Базовые операции numpy / np 3
Содержание:
- Выгодно ли писать стихи за деньги, и как начать зарабатывать?
- Нам доверяют
- Как создаются матрицы в Python?
- Функции, определенные для массивов¶
- Полиномы (numpy.polynomial)¶
- 7.4. Генерация случайных значений
- Навигация по записям
- Решение системы линейных уравнений
- Создание матрицы
- Заполнение матрицы произвольными значениями
- Вывод матрицы на экран
- Создание списков на Python
- Пакеты в SciPy
- Изменяем количество строк матрицы. Данные не меняются
- 1.1. Автозаполнение массивов
- Runtastic
- Использование модуля pickle на своих объектах
Выгодно ли писать стихи за деньги, и как начать зарабатывать?
Если оглянуться на десятки и сотни лет назад, то можно сказать, что ни поэты, ни писатели не имели таких заработков, которыми обладают современные «ваятели». А почему? Потому что они писали от души, излагали на бумаге то, что чувствовали. А это не было нужно ни тогда, ни сейчас. Ценились только стихи и рассказы придворных писателей и поэтов.
Что из этого следует? Вывод однозначен: если вы хотите продавать стихи в интернете, чтобы их покупали, а не чтобы они «висели» в вашем виртуальном магазине, пишите их под заказ. Это можно сделать 2 способами:
- Зарегистрироваться на специальном сайте (или сразу нескольких), где вы сможете продавать стихи собственного сочинения за деньги. Кстати, сегодня таким способом можно заработать и на многочисленных биржах копирайтинга, а не только на ресурсах, созданных исключительно для поэтов или писателей.
- Начать сотрудничество с фирмами, которые скупают поэзию оптом. Если вы выберете такой способ продажи стихов, то будьте готовыми к тому, что такие организации могут использовать их в своих целях, в том числе и для дальнейшей перепродажи по более высокой стоимости.
Еще один вариант, как продавать свои стихи, – это связаться с администрацией виртуальных или печатных изданий. Конечно, вполне возможно, что такой способ заработка может потребовать от вас некоторых вложений. Но потом, когда вы станете постоянным автором, написание стихов на заказ начнет приносить вам реальный заработок.
Нам доверяют
Как создаются матрицы в Python?
Добавление и модификация массивов или матриц (matrix) в Python осуществляется с помощью библиотеки NumPy. Вы можете создать таким образом и одномерный, и двумерный, и многомерный массив. Библиотека обладает широким набором пакетов, которые необходимы, чтобы успешно решать различные математические задачи. Она не только поддерживает создание двумерных и многомерных массивов, но обеспечивает работу однородных многомерных матриц.
Чтобы получить доступ и начать использовать функции данного пакета, его импортируют:
import numpy as np
Функция array() — один из самых простых способов, позволяющих динамически задать одно- и двумерный массив в Python. Она создаёт объект типа ndarray:
array = np.array(/* множество элементов */)
Для проверки используется функция array.type() — принимает в качестве аргумента имя массива, который был создан.
Если хотите сделать переопределение типа массива, используйте на стадии создания dtype=np.complex:
array2 = np.array([ /*элементы*/, dtype=np.complex)
Когда стоит задача задать одномерный или двумерный массив определённой длины в Python, и его значения на данном этапе неизвестны, происходит его заполнение нулями функцией zeros(). Кроме того, можно получить матрицу из единиц через функцию ones(). При этом в качестве аргументов принимают число элементов и число вложенных массивов внутри:
np.zeros(2, 2, 2)
К примеру, так в Python происходит задание двух массивов внутри, которые по длине имеют два элемента:
array(] ]] )
Если хотите вывести одно- либо двумерный массив на экран, вам поможет функция print(). Учтите, что если матрица слишком велика для печати, NumPy скроет центральную часть и выведет лишь крайние значения. Дабы увидеть массив полностью, используется функция set_printoptions(). При этом по умолчанию выводятся не все элементы, а происходит вывод только первой тысячи. И это значение массива указывается в качестве аргумента с ключевым словом threshold.
Функции, определенные для массивов¶
Алгебраические функции
| Функця | Описание |
|---|---|
| isreal(x) | проверка на действительность (по элементам) |
| iscomplex(x) | проверка на комплексность (по элементам) |
| isfinite(x) | приверка элементов на числовое значение (не бесконечность и не «не число»). |
| isinf(x) | проверка на бесконечность (по элементам) |
| isnan(x) | проверка аргумента на «не число» (NaN), результат – логический массив |
| signbit(x) | истина, если установлен бит знака (меньше нуля) |
| copysign(x1, x2) | меняет знак x1 на знак x2 (по элементам |
| nextafter(x1, x2) | следующее в направлении x2 число, представимое в виде с плавающей точкой (по элементам) |
| modf(x) | дробная и целая часть числа |
| ldexp(x1, x2) | вычисляет y = x1 * 2**x2. |
| frexp(x) | разделение числа на нормированную часть и степень |
| absolute(x) | Calculate the absolute value element-wise. |
| rint(x) | округление элементов массива |
| trunc(x) | отбрасывание дробной части (по элементам) |
| floor(x) | целая часть |
| ceil(x) | минимальное целое большее числа |
| sign(x) | знаки элементов |
| conj(x) | комплексное сопряжение (по элементам). |
| exp(x) | экспонента (по элементам) |
| exp2(x) | 2**элемент (по элементам) |
| log(x) | натуральный логарифм (по элементам) |
| log2(x) | двоичный логарифм (по элементам) |
| log10(x) | десятичный логарифм (по элементам) |
| expm1(x) | exp(x) — 1 (по элементам) |
| log1p(x) | Return the natural logarithm of one plus the input array, element-wise. |
| sqrt(x) | квадратный корень (для положительных) (по элементам) |
| square(x) | квадрат (по элементам) |
| reciprocal(x) | обратная величина (по элементам) |
- x – массив
- out – место для результата
Тригонометрические функции
Все тригонометрические функции работают с радианами.
| Функция | Обратная функция | Описание |
|---|---|---|
| sin(x) | arcsin(x) | синус (по элементам) |
| cos(x) | arccos(x) | косинус (по элементам) |
| tan(x) | arctan(x) | тангенс (по элементам) |
| arctan2(x1, x2) | арктангенс x1/x2 с правильным выбором четверти (по элементам) | |
| hypot(x1, x2) | гипотенуза по двум катетам (по элементам) | |
| sinh(x) | arcsinh(x) | гиперболический синус (по элементам) |
| cosh(x) | arccosh(x) | гиперболический косинус (по элементам) |
| tanh(x) | arctanh(x) | гиперболический тангенс (по элементам) |
| deg2rad(x) | rad2deg(x) | преобразование градусов в радианы (по элементам) |
- x, x1, x2 – массивы
- out – место для результата
Функции двух аргументов (бинарные функции)
Для правильной работы с логическими бинарными функциям (AND, OR) необходимо явно их записывать через функции
модуля «NumPy», а не полагаться на встроенные функции питона.
| Функция | Описание |
|---|---|
| add(x1, x2) | сумма (по элементам) |
| subtract(x1, x2) | разность (по элементам) |
| multiply(x1, x2) | произведение (по элементам) |
| divide(x1, x2) | деление (по элементам) |
| logaddexp(x1, x2) | логарифм суммы экспонент (по элементам) |
| logaddexp2(x1, x2) | логарифм по основанию 2 от суммы экспонент (по элементам) |
| true_divide(x1, x2) | истинное деление (с преобразованием типов) |
| floor_divide(x1, x2) | деление без преобразования типов (целочисленное) |
| negative(x) | обратные элементы (по элементам) |
| power(x1, x2) | элементы первого массива в степени элементов из второго массива (по элементам) |
| remainder(x1, x2), mod(x1, x2), fmod(x1, x2) | остаток от деления (по элементам). |
| greater(x1, x2) | истина, если (x1 > x2) (по элементам). |
| greater_equal(x1, x2) | истина, если (x1 > =x2) (по элементам). |
| less(x1, x2) | истина, если (x1 < x2) (по элементам). |
| less_equal(x1, x2) | истина, если (x1 =< x2) (по элементам). |
| not_equal(x1, x2) | истина, если (x1 != x2) (по элементам). |
| equal(x1, x2) | истина, если (x1 == x2) (по элементам). |
| logical_and(x1, x2) | истина, если (x1 AND x2) (по элементам). |
| logical_or(x1, x2) | истина, если (x1 OR x2) (по элементам). |
| logical_xor(x1, x2) | истина, если (x1 XOR x2) (по элементам). |
| logical_not(x) | истина, если (NOT x1) (по элементам). |
| maximum(x1, x2) | максимум из элементов двух массивов(по элементам). |
- x1, x2 – массивы
- out – место для результата
Бинарные функции поддерживают дополнительные методы, позволяющие накапливать значения результата различными
способами.
- accumulate() Аккумулирование результата.
- outer() Внешнее «произведение».
- reduce() Сокращение.
- reduceat() Сокращение в заданных точках.
Методы accumulate(), reduce() и reduceat() принимают необязательный аргумент — номер размерности, используемой
для соответствующего действия. По умолчанию применяется нулевая размерность.
Полиномы (numpy.polynomial)¶
Модуль полиномов обеспечивает стандартные функции работы с полиномами разного вида. В нем реализованы полиномы
Чебышева, Лежандра, Эрмита, Лагерра. Для полиномов определены стандартные арифметические функции ‘+’, ‘-‘, ‘*’, ‘//’,
деление по модулю, деление с остатком, возведение в степень и вычисление значения полинома
Важно задавать область
определения, т.к. часто свойства полинома (например при интерполяции) сохраняются только на определенном интервале.
В зависимости от класса полинома, сохраняются коэффициенты разложения по полиномам определенного типа, что позволяет
получать разложение функций в ряд по полиномам разного типа
| Типы полиномов | Описание |
|---|---|
| Polynomial(coef) | разложение по степеням «x» |
| Chebyshev(coef) | разложение по полиномам Чебышева |
| Legendre(coef) | разложение по полиномам Лежандра |
| Hermite(coef) | разложение по полиномам Эрмита |
| HermiteE(coef) | разложение по полиномам Эрмита_Е |
| Laguerre(coef) | разложение по полиномам Лагерра |
- coef – массив коэффициентов в порядке увеличения
- domain – область определения проецируется на окно
- window – окно. Сдвигается и масштабируется до размера области определения
Некоторые функции (например интерполяция данных) возвращают объект типа полином. У этого объекта есть набор методов,
позволяющих извлекать и преобразовывать данные.
| Методы полиномов | Описание |
|---|---|
| __call__(z) | полином можно вызвать как функцию |
| convert() | конвертирует в полином другого типа, с другим окном и т.д |
| copy() | возвращает копию |
| cutdeg(deg) | обрезает полином до нужной степени |
| degree() | возвращает степень полинома |
| deriv() | вычисляет производную порядка m |
| fit(x, y, deg) | формирует полиномиальную интерполяцию степени deg для данных (x,y) по методу наименьших квадратов |
| fromroots(roots) | формирует полином по заданным корням |
| has_samecoef(p) | проверка на равенство коэффициентов. |
| has_samedomain(p) | проверка на равенство области определения |
| has_samewindow(p) | проверка на равенство окна |
| integ() | интегрирование |
| linspace() | возвращает x,y — значения на равномерной сетке по области определения |
| mapparms() | возвращает коэффициенты масштабирования |
| roots() | список корней |
| trim() | создает полином с коэффициентами большими tol |
| truncate(size) | ограничивает ряд по количеству коеффициентов |
- p – полином
- x, y – набор данных для аппроксимации
- deg – степень полинома
- domain – область определения
- rcond – относительное число обусловленности элементы матрицы интерполяции с собственными значениями меньшими данного будут отброшены.
- full – выдавать дополнительную информацию о качестве полинома
- w – веса точек
- window – окно
- roots – набор корней
- m – порядок производной (интеграла)
- k – константы интегрирования
- lbnd – нижняя граница интервала интегрирования
- n – число точек разбиения
- size – число ненулевых коэффициентов
7.4. Генерация случайных значений
Очень многие вычислительные методы требуют генерации случайных значений. В некоторых ситуациях, на генерируемые данные накладываются очень строгие и высокие требования. NumPy содержит функции для генерации простых случайных данных, функции генерации случайных перестановок, а так же большое количество функций для гернерации случайных чисел с всевозможными вероятностными распределениями.
Получение простых случайных данных:
Перестановки:
NumPy предоставляет порядка 30 функций, позволяющих генерировать случайные числа с самыми разными вероятностными распределениями:
Вы так же имеете доступ к состоянию генератора случайных чисел, а так же можете управлять им:
Навигация по записям
Решение системы линейных уравнений
http-equiv=»Content-Type» content=»text/html;charset=UTF-8″>kquote class=»wp-block-quote»>
В заключение мы рассмотрим последнюю из самых распространённых операций с матрицами – решение системы линейных уравнений.
Напомню, что система линейных уравнений имеет вид
где A – матрица, x – вектор-столбец искомых значений, b – вектор чисел. Решение, конечно же, состоит в умножении обоих частей уравнений на матрицу, обратную A:
Это корректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что она обратима. Тогда x имеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.
Тут не должно возникнуть никаких сложностей, поскольку у нас уже есть весь инструментарий, необходимый для такого рода вычислений. Вы уже видели, как находится обратная матрица и как производить умножение матриц, а именно эти две вещи нам и нужны.
Решим пример. A у нас будет матрицей
Это корректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что она обратима. Тогда x имеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.
Тут не должно возникнуть никаких сложностей, поскольку у нас уже есть весь инструментарий, необходимый для такого рода вычислений. Вы уже видели, как находится обратная матрица и как производить умножение матриц, а именно эти две вещи нам и нужны.
Решим пример. A у нас будет матрицей
b у нас будет вектором :
b = np.array()
Решением будет
x = np.linalg.inv(A).dot(b)
Итак, решением являются числа 0 и 0,5. Для проверки попробуйте решить этот пример вручную.
Конечно же, ввиду очень частого проведения такого рода вычислений, есть способ и получше – с помощью функции с соответствующим названием solve. Поэтому можно записать
x = np.linalg.solve(A, b)
И получим тот же ответ.
Если вы когда-либо прежде писали код в MATLAB, то могли заметить, что при попытке использовать метод inv MATLAB выдаёт предупреждение и сообщает, что есть и более эффективный способ вычислений. В MATLAB он называется не solve, но по сути это тот же самый алгоритм, и он действительно куда более эффективен и точен. Поэтому если у вас когда-нибудь возникнет необходимость решить подобного рода уравнение, никогда не пользуетесь inv. Всегда используйте solve.
Текстовая задача
Давайте разберём несложный пример, чтобы попрактиковаться в использовании функции solve.
Итак, поставим задачу. На небольшой ярмарке входная плата составляет 1,5 доллара для ребёнка и 4 доллара для взрослого. Однажды за день ярмарку посетило 2200 человек; при этом было собрано 5050 долларов входной платы. Сколько детей и сколько взрослых посетили ярмарку в этот день?
Итак, обозначим количество детей через X1, а количество взрослых – через X2. Мы знаем, что
Мы также знаем, что
Мы также знаем, что
Обратите внимание, что это линейное уравнение, где A равно:
а b равно :
а b равно :
Подставим эти значения в Numpy и найдём решение:
A = np.array(, ])
b = np.array()
np.linalg.solve(A, b)
Получаем ответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнение вручную, чтобы проверить ответ.
Создание матрицы
Вариант 1: Строгое задание элементов матрицы
arr = , ]
arr = , ]
Вариант 2. Создание в памяти матрицы заданного размера, заполненной некоторыми начальными значениями (например, нулями)
НЕВЕРНЫЙ способ (так делать точно не надо)
row = * M
A = * N
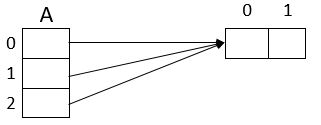
ДЕЛАЕМ ПРАВИЛЬНО!
Чтобы создать правильно матрицу, необходимо заставить компилятор создать все строки в памяти как разные объекты.
Для этого необходимо сначала создать пустой список, а затем в цикле добавлять к нему новые строки с помощью метода
N = 3 M = 2 A = [] for i in range(N): A.append(*M)
сделать то же самое можно с помощью генератора
N = 3 M = 2 A = *M for i in range(N) ]
Заполнение матрицы произвольными значениями
После создания матрицы можно заполнить ее произвольными значениями. Так как каждый элемент имеет два индекса, то необходимо использовать вложенные циклы
for i in range(N):
for j in range(M):
A = ...
Вывод матрицы на экран
Вариант 1. Простейший способ
Вывод матрицы в одну строку
print(A)
Вариант 2.
Для обработки и вывода списка, как правило, используется два вложенных цикла. Первый цикл по номеру строки, второй цикл — по элементам внутри строки.
Для того, чтобы вывести матрицу на экран построчно, разделяя числа пробелами внутри одной строки, необходимо написать такой фрагмент:
for i in range(len(A)): # len(A) - возвращает количество строк в матрице А
for j in range(len(A)): # len(A) - возвращает количество элементов в строке i
print(A, end = ' ')
print() # делаем переход на новую строку после вывода на экран строки
То же самое, но циклы не по индексу, а по значениям списка (цикл for умеет делать перебор всех элементов в списке (массиве), строке):
for row in A: # делаем перебор всех строк матрицы A
for elem in row: # перебираем все элементы в строке row
print(elem, end = ' ')
print()
Для вывода одной строки можно воспользоваться методом :
for row in A:
print(' '.join(list(map(str, row))))
Создание списков на Python
- Создать список можно несколькими способами. Рассмотрим их.
1. Получение списка через присваивание конкретных значений
Так выглядит в коде Python пустой список:
s = # Пустой список |
Примеры создания списков со значениями:
l = 25, 755, -40, 57, -41 # список целых чисел l = 1.13, 5.34, 12.63, 4.6, 34.0, 12.8 # список из дробных чисел l = "Sveta", "Sergei", "Ivan", "Dasha" # список из строк l = "Москва", "Иванов", 12, 124 # смешанный список l = , , , 1, , 1, 1, 1, # список, состоящий из списков l = 's', 'p', 'isok', 2 # список из значений и списка |
2. Списки при помощи функции List()
Получаем список при помощи функции List()
empty_list = list() # пустой список
l = list ('spisok') # 'spisok' - строка
print(l) # - результат - список
|
4. Генераторы списков
- В python создать список можно также при помощи генераторов, — это довольно-таки новый метод:
- Первый простой способ.
Сложение одинаковых списков заменяется умножением:
# список из 10 элементов, заполненный единицами l = 1*10 # список l = |
Второй способ сложнее.
l = i for i in range(10) # список l = |
или такой пример:
c = c * 3 for c in 'list' print (c) # |
Пример:
Заполнить список квадратами чисел от 0 до 9, используя генератор списка.
Решение:
l = i*i for i in range(10) |
еще пример:
l = (i+1)+i for i in range(10) print(l) # |
Случайные числа в списке:
from random import randint l = randint(10,80) for x in range(10) # 10 чисел, сгенерированных случайным образом в диапазоне (10,80) |
Задание Python 4_1:
Создайте список целых чисел от -20 до 30 (генерация).
Результат:
Задание Python 4_2:
Создайте список целых чисел от -10 до 10 с шагом 2 (генерация list).
Результат:
Задание Python 4_3:
Создайте список из 20 пятерок (генерация).
Результат:
Задание Python 4_4:
Создайте список из сумм троек чисел от 0 до 10, используя генератор списка (0 + 1 + 2, 1 + 2 + 3, …).
Результат:
Задание Python 4_5 (сложное):
Заполните массив элементами арифметической прогрессии. Её первый элемент, разность и количество элементов нужно ввести с клавиатуры.
* Формула для получения n-го члена прогрессии: an = a1 + (n-1) * d
Простейшие операции над списками
- Списки можно складывать (конкатенировать) с помощью знака «+»:
l = 1, 3 + 4, 23 + 5 # Результат: # l = |
33, -12, 'may' + 21, 48.5, 33 # |
или так:
a=33, -12, 'may' b=21, 48.5, 33 print(a+b)# |
Операция повторения:
,,,1,1,1 * 2 # , , , , , ] |
Пример:
Для списков операция переприсваивания значения отдельного элемента списка разрешена!:
a=3, 2, 1 a1=; print(a) # |
Можно!
Задание 4_6:
В строке записана сумма натуральных чисел: ‘1+25+3’. Вычислите это выражение. Работать со строкой, как со списком.
Начало программы:
s=input('введите строку')
l=list(str(s));
|
Как узнать длину списка?
Пакеты в SciPy
В SciPy есть набор пакетов для разных научных вычислений:
| Название | Описание |
|---|---|
| Алгоритмы кластерного анализа | |
| Физические и математические константы | |
| Быстрое преобразование Фурье | |
| Решения интегральных и обычных дифференциальных уравнений | |
| Интерполяция и сглаживание сплайнов | |
| Ввод и вывод | |
| Линейная алгебра | |
| N-размерная обработка изображений | |
| Метод ортогональных расстояний | |
| Оптимизация и численное решение уравнений | |
| Обработка сигналов | |
| Разреженные матрицы | |
| Разреженные и алгоритмы | |
| Специальные функции | |
| Статистические распределения и функции |
Подробное описание можно найти в официальной документации.
Эти пакеты нужно импортировать для использования библиотеки. Например:
Прежде чем рассматривать каждую функцию в подробностях, разберемся с теми из них, которые являются одинаковыми в NumPy и SciPy.
Изменяем количество строк матрицы. Данные не меняются
ravel, reshape, T
In : numpy as np
In : a = np.array(,
...:
...: ])
In : a
Out:
array(,
])
In : a.shape
Out: (2, 3)
In : a.ravel()
Out: array()
In : a.reshape(3,2)
Out:
array(,
,
])
In : a.reshape(3, -1)
Out:
array(,
,
])
In : a.T
Out:
array(,
,
])
In : np.transpose(a)
Out:
array(,
,
])
vstack, hstack, вектор строкой и столбцом, column_stack
In : b = np.array()
Out: array()
In : v = b
Out:
array(,
,
,
])
In : bm = np.vstack((b, b, b))
Out:
array(,
,
])
In : bs = np.hstack((b, b, b))
Out: array()
In : np.column_stack((b, b))
Out:
array(,
,
,
])
In : a1 = np.array(, ])
Out:
array(,
])
In : a2 = np.array(])
Out: array(])
In : np.concatenate((a1, a2), axis= 0)
Out:
array(,
,
])
In : a2.T
Out:
array(,
])
In : np.concatenate((a1, a2.T), axis= 1)
Out:
array(,
])
np.hsplit
np.vsplit
делим НА 3 части
np.hsplit(массив, n)
In : a = np.arange(1, 25)
Out:
array()
In : a1 = a.reshape((2, 12))
Out:
array(,
])
In : np.hsplit(a1, 3)
Out:
,
]), array(,
]), array(,
])]
In : s1 = np.hsplit(a1, 3)
In : s1
Out:
array(,
])
In : s1
Out:
array(,
])
In : s1
Out:
array(,
])
делим ПОСЛЕ столбцов номер (n1, n2, n3 и далее)
np.hsplit(массив, (3, 4))
In : a = np.arange(1, 25)
Out:
array()
In : a1 = a.reshape((2, 12))
Out:
array(,
])
In : w1 = np.hsplit(a1, (3, 4))
In : w1
Out:
,
]), array(,
]), array(,
])]
In : w1
Out:
array(,
])
In : w1
Out:
array(,
])
In : w1
Out:
array(,
])
1.1. Автозаполнение массивов
- Возвращает новый массив заданной формы и типа без инициированных записей.
- Возвращает новый массив с формой и типом данных указанного массива без инициированных записей.
- Возвращает новый массив в котором диагональные элементы равны единице, а все остальные равны нулю.
- Возвращает новый квадратный массив с единицами по главной диагонали.
- Возвращает новый массив заданной формы и типа, заполненный единицами.
- Возвращает новый массив с формой и типом данных указанного массива, заполненный единицами.
- Возвращает новый массив заданной формы и типа, заполненный нулями.
- Возвращает новый массив с формой и типом данных указанного массива, заполненный нулями.
- Возвращает новый массив заданной формы и типа все элементы которого равны указанному значению.
- Возвращает новый массив с формой и типом данных указанного массива, все элементы которого равны указанному значению.
Runtastic
Использование модуля pickle на своих объектах
протокол
Сериализация собственных объектов.
-
Если вы хотите, чтобы после десериализации вашего класса был вызыван , вы можете определить , который должен вернуть кортеж аргументов, который будет отправлен в . Заметьте, что этот метод работает только с классами старого стиля.
-
Для классов нового стиля вы можете определить, какие параметры будут переданы в во время десериализации. Этот метод так же должен вернуть кортеж аргументов, которые будут отправлены в .
-
Вместо стандартного атрибута , где хранятся атрибуты класса, вы можете вернуть произвольные данные для сериализации. Эти данные будут переданы в во время десериализации.
-
Если во время десериализации определён , то данные объекта будут переданы сюда, вместо того чтобы просто записать всё в . Это парный метод для : когда оба определены, вы можете представлять состояние вашего объекта так, как вы только захотите.
-
Если вы определили свой тип (с помощью Python’s C API), вы должны сообщить Питону как его сериализовать, если вы хотите, чтобы он его сериализовал. вызывается когда сериализуется объект, в котором этот метод был определён. Он должен вернуть или строку, содержащую имя глобальной переменной, содержимое которой сериализуется как обычно, или кортеж. Кортеж может содержать от 2 до 5 элементов: вызываемый объект, который будет вызван, чтобы создать десериализованный объект, кортеж аргументов для этого вызываемого объекта, данные, которые будут переданы в (опционально), итератор списка элементов для сериализации (опционально) и итератор словаря элементов для сериализации (опционально).
-
Иногда полезно знать версию протокола, реализуя . И этого можно добиться, реализовав вместо него . Если реализован, то предпочтение при вызове отдаётся ему (вы всё-равно должны реализовать для обратной совместимости).