Numpy, часть 1: начало работы
Содержание:
- Implementing MergeSort and QuickSort
- Массив нарезки
- Двумерный массив
- Создание массивов
- Array Methods
- Многомерный массив
- Алгоритм быстрой сортировки
- Транспонирование и изменение формы матриц в numpy
- Добавление нового массива
- Python NumPy
- Python Tutorial
- Индексирование массивов
- 1.1. Автозаполнение массивов
- Примеры работы с NumPy
- Создание, вывод и ввод матрицы в Питоне
Implementing MergeSort and QuickSort
Here, we investigate two other commonly used Sorting techniques used in actual practice, namely the MergeSort and the QuickSort algorithms.
1. MergeSort Algorithm
The algorithm uses a bottom-up Divide and Conquer approach, first dividing the original array into subarrays and then merging the individually sorted subarrays to yield the final sorted array.
In the below code snippet, the method does the actual splitting into subarrays and the perform_merge() method merges two previously sorted arrays into a new sorted array.
import array
def mergesort(a, arr_type):
def perform_merge(a, arr_type, start, mid, end):
# Merges two previously sorted arrays
# a and a
tmp = array.array(arr_type, )
def compare(tmp, i, j):
if tmp <= tmp:
i += 1
return tmp
else:
j += 1
return tmp
i = start
j = mid + 1
curr = start
while i<=mid or j<=end:
if i<=mid and j<=end:
if tmp <= tmp:
a = tmp
i += 1
else:
a = tmp
j += 1
elif i==mid+1 and j<=end:
a = tmp
j += 1
elif j == end+1 and i<=mid:
a = tmp
i += 1
elif i > mid and j > end:
break
curr += 1
def mergesort_helper(a, arr_type, start, end):
# Divides the array into two parts
# recursively and merges the subarrays
# in a bottom up fashion, sorting them
# via Divide and Conquer
if start < end:
mergesort_helper(a, arr_type, start, (end + start)//2)
mergesort_helper(a, arr_type, (end + start)//2 + 1, end)
perform_merge(a, arr_type, start, (start + end)//2, end)
# Sorts the array using mergesort_helper
mergesort_helper(a, arr_type, 0, len(a)-1)
Test Case:
a = array.array('i', )
print('Before MergeSort ->', a)
mergesort(a, 'i')
print('After MergeSort ->', a)
Output:
Before MergeSort -> array('i', )
After MergeSort -> array('i', )
2. QuickSort Algorithm
This algorithm also uses a Divide and Conquer strategy, but uses a top-down approach instead, first partitioning the array around a pivot element (here, we always choose the last element of the array to be the pivot).
Thus ensuring that after every step, the pivot is at its designated position in the final sorted array.
After ensuring that the array is partitioned around the pivot (Elements lesser than the pivot are to the left, and the elements which are greater than the pivot are to the right), we continue applying the function to the rest of the array, until all the elements are at their respective position, which is when the array is completely sorted.
Note: There are other approaches to this algorithm for choosing the pivot element. Some variants choose the median element as the pivot, while others make use of a random selection strategy for the pivot.
def quicksort(a, arr_type):
def do_partition(a, arr_type, start, end):
# Performs the partitioning of the subarray a
# We choose the last element as the pivot
pivot_idx = end
pivot = a
# Keep an index for the first partition
# subarray (elements lesser than the pivot element)
idx = start - 1
def increment_and_swap(j):
nonlocal idx
idx += 1
a, a = a, a
< pivot]
# Finally, we need to swap the pivot (a with a)
# since we have reached the position of the pivot in the actual
# sorted array
a, a = a, a
# Return the final updated position of the pivot
# after partitioning
return idx+1
def quicksort_helper(a, arr_type, start, end):
if start < end:
# Do the partitioning first and then go via
# a top down divide and conquer, as opposed
# to the bottom up mergesort
pivot_idx = do_partition(a, arr_type, start, end)
quicksort_helper(a, arr_type, start, pivot_idx-1)
quicksort_helper(a, arr_type, pivot_idx+1, end)
quicksort_helper(a, arr_type, 0, len(a)-1)
Here, the method does the step of the Divide and Conquer approach, while the method partitions the array around the pivot and returns the position of the pivot, around which we continue to recursively partition the subarray before and after the pivot until the entire array is sorted.
Test Case:
b = array.array('i', )
print('Before QuickSort ->', b)
quicksort(b, 'i')
print('After QuickSort ->', b)
Output:
Before QuickSort -> array('i', )
After QuickSort -> array('i', )
Массив нарезки
Все идет нормально; Создание и индексация массивов выглядит знакомо.
Теперь мы подошли к нарезке массивов, и это одна из функций, которая создает проблемы для начинающих массивов Python и NumPy.
Структуры, такие как списки и массивы NumPy, могут быть нарезаны. Это означает, что подпоследовательность структуры может быть проиндексирована и извлечена.
Это наиболее полезно при машинном обучении при указании входных и выходных переменных или разделении обучающих строк из строк тестирования.
Нарезка задается с помощью оператора двоеточия ‘:’ с ‘от’ а также ‘в‘Индекс до и после столбца соответственно. Срез начинается от индекса «от» и заканчивается на один элемент перед индексом «до».
Давайте рассмотрим несколько примеров.
Одномерная нарезка
Вы можете получить доступ ко всем данным в измерении массива, указав срез «:» без индексов.
При выполнении примера печатаются все элементы в массиве.
Первый элемент массива можно разрезать, указав фрагмент, который начинается с индекса 0 и заканчивается индексом 1 (один элемент перед индексом «до»)
Выполнение примера возвращает подмассив с первым элементом.
Мы также можем использовать отрицательные индексы в срезах. Например, мы можем нарезать последние два элемента в списке, начав срез с -2 (второй последний элемент) и не указав индекс «до»; это берет ломтик до конца измерения.
Выполнение примера возвращает подмассив только с двумя последними элементами.
Двумерная нарезка
Давайте рассмотрим два примера двумерного среза, которые вы, скорее всего, будете использовать в машинном обучении.
Разделение функций ввода и вывода
Распространено загруженные данные на входные переменные (X) и выходную переменную (y).
Мы можем сделать это, разрезая все строки и все столбцы до, но перед последним столбцом, затем отдельно индексируя последний столбец.
Для входных объектов мы можем выбрать все строки и все столбцы, кроме последнего, указав ‘:’ в индексе строк и: -1 в индексе столбцов.
Для выходного столбца мы можем снова выбрать все строки, используя ‘:’, и индексировать только последний столбец, указав индекс -1.
Собрав все это вместе, мы можем разделить 3-колоночный 2D-набор данных на входные и выходные данные следующим образом:
При выполнении примера печатаются разделенные элементы X и y
Обратите внимание, что X — это двумерный массив, а y — это одномерный массив
Сплит поезд и тестовые ряды
Обычно загруженный набор данных разбивают на отдельные наборы поездов и тестов.
Это разделение строк, где некоторая часть будет использоваться для обучения модели, а оставшаяся часть будет использоваться для оценки мастерства обученной модели.
Для этого потребуется разрезать все столбцы, указав «:» во втором индексе измерения. Набор обучающих данных будет содержать все строки от начала до точки разделения.
Тестовым набором данных будут все строки, начиная с точки разделения до конца измерения.
Собрав все это вместе, мы можем разделить набор данных в надуманной точке разделения 2.
При выполнении примера выбираются первые две строки для обучения и последняя строка для набора тестов.
Двумерный массив
В некоторых случаях для правильного представления определенного набора информации обычного одномерного массива оказывается недостаточно. В языке программирования Python 3 двумерных и многомерных массивов не существует, однако базовые возможности этой платформы легко позволяют построить двумерный список. Элементы подобной конструкции располагаются в столбцах и строках, заполняемых как это показано на следующем примере.
d1 = [] for j in range(5): d2 = [] for i in range(5): d2.append(0) d1.append(d2)
Здесь можно увидеть, что основная идея реализации двумерного набора данных заключается в создании нескольких списков d2 внутри одного большого списка d1. При помощи двух циклов for происходит автоматическое заполнение нулями матрицы с размерностью 5×5. С этой задачей помогают справляться методы append и range, первый из которых добавляет новый элемент в список (0), а второй позволяет устанавливать его величину (5). Нельзя не отметить, что для каждого нового цикла for используется собственная временная переменная, выполняющая представление текущего элемента внешнего (j) или внутренних (i) списков. Обратиться к нужной ячейке многомерного списка можно при помощи указания ее координат в квадратных скобках, ориентируясь на строки и столбцы: d1.
Создание массивов
В NumPy существует много способов создать массив. Один из наиболее простых — создать массив из обычных списков или кортежей Python, используя функцию numpy.array() (запомните: array — функция, создающая объект типа ndarray):
>>> import numpy as np >>> a = np.array() >>> a array() >>> type(a) <class 'numpy.ndarray'>
Функция array() трансформирует вложенные последовательности в многомерные массивы. Тип элементов массива зависит от типа элементов исходной последовательности (но можно и переопределить его в момент создания).
>>> b = np.array(, 4, 5, 6]])
>>> b
array(,
])
Можно также переопределить тип в момент создания:
>>> b = np.array(, 4, 5, 6]], dtype=np.complex)
>>> b
array(,
])
Функция array() не единственная функция для создания массивов. Обычно элементы массива вначале неизвестны, а массив, в котором они будут храниться, уже нужен. Поэтому имеется несколько функций для того, чтобы создавать массивы с каким-то исходным содержимым (по умолчанию тип создаваемого массива — float64).
Функция zeros() создает массив из нулей, а функция ones() — массив из единиц. Обе функции принимают кортеж с размерами, и аргумент dtype:
>>> np.zeros((3, 5))
array(,
,
])
>>> np.ones((2, 2, 2))
array(,
],
,
]])
Функция eye() создаёт единичную матрицу (двумерный массив)
>>> np.eye(5)
array(,
,
,
,
])
Функция empty() создает массив без его заполнения. Исходное содержимое случайно и зависит от состояния памяти на момент создания массива (то есть от того мусора, что в ней хранится):
>>> np.empty((3, 3))
array(,
,
])
>>> np.empty((3, 3))
array(,
,
])
Для создания последовательностей чисел, в NumPy имеется функция arange(), аналогичная встроенной в Python range(), только вместо списков она возвращает массивы, и принимает не только целые значения:
>>> np.arange(10, 30, 5) array() >>> np.arange(, 1, 0.1) array()
Вообще, при использовании arange() с аргументами типа float, сложно быть уверенным в том, сколько элементов будет получено (из-за ограничения точности чисел с плавающей запятой). Поэтому, в таких случаях обычно лучше использовать функцию linspace(), которая вместо шага в качестве одного из аргументов принимает число, равное количеству нужных элементов:
>>> np.linspace(, 2, 9) # 9 чисел от 0 до 2 включительно array()
fromfunction(): применяет функцию ко всем комбинациям индексов
Array Methods
Python has a set of built-in methods that you can use on lists/arrays.
| Method | Description |
|---|---|
| append() | Adds an element at the end of the list |
| clear() | Removes all the elements from the list |
| copy() | Returns a copy of the list |
| count() | Returns the number of elements with the specified value |
| extend() | Add the elements of a list (or any iterable), to the end of the current list |
| index() | Returns the index of the first element with the specified value |
| insert() | Adds an element at the specified position |
| pop() | Removes the element at the specified position |
| remove() | Removes the first item with the specified value |
| reverse() | Reverses the order of the list |
| sort() | Sorts the list |
Note: Python does not have built-in support for Arrays,
but Python Lists can be used instead.
❮ Previous
Next ❯
Многомерный массив
Как и в случае с двумерным массивом, представленным в виде сложного списка, многомерный массив реализуется по принципу «списков внутри списка». Следующий пример наглядно демонстрирует создание трехмерного списка, который заполняется нулевыми элементами при помощи трех циклов for. Таким образом, программа создает матрицу с размерностью 5×5×5.
d1 = []
for k in range(5):
d2 = []
for j in range(5):
d3 = []
for i in range(5):
d3.append(0)
d2.append(d3)
d1.append(d3)
Аналогично двумерному массиву, обратиться к ячейке построенного выше объекта можно с помощью индексов в квадратных скобках, например, d1.
Алгоритм быстрой сортировки
Этот алгоритм также использует разделяй и стратегию завоюйте, но использует подход сверху вниз вместо первого разделения массива вокруг шарнирного элемента (здесь, мы всегда выбираем последний элемент массива будут стержень).
Таким образом гарантируется, что после каждого шага точка поворота находится в назначенной позиции в окончательном отсортированном массиве.
Убедившись, что массив разделен вокруг оси поворота (элементы, меньшие точки поворота, находятся слева, а элементы, которые больше оси поворота, находятся справа), мы продолжаем применять функцию к остальной части, пока все элементы находятся в соответствующих позициях, когда массив полностью отсортирован.
def quicksort(a, arr_type):
def do_partition(a, arr_type, start, end):
# Performs the partitioning of the subarray a
# We choose the last element as the pivot
pivot_idx = end
pivot = a
# Keep an index for the first partition
# subarray (elements lesser than the pivot element)
idx = start - 1
def increment_and_swap(j):
nonlocal idx
idx += 1
a, a = a, a
< pivot]
# Finally, we need to swap the pivot (a with a)
# since we have reached the position of the pivot in the actual
# sorted array
a, a = a, a
# Return the final updated position of the pivot
# after partitioning
return idx+1
def quicksort_helper(a, arr_type, start, end):
if start < end:
# Do the partitioning first and then go via
# a top down divide and conquer, as opposed
# to the bottom up mergesort
pivot_idx = do_partition(a, arr_type, start, end)
quicksort_helper(a, arr_type, start, pivot_idx-1)
quicksort_helper(a, arr_type, pivot_idx+1, end)
quicksort_helper(a, arr_type, 0, len(a)-1)
Здесь метод выполняет шаг подхода Divide and Conquer, в то время метод разделяет массив вокруг точки поворота и возвращает позицию точки поворота, вокруг которой мы продолжаем рекурсивно разбивать подмассив до и после точки поворота, пока не будет весь массив отсортирован.
Прецедент:
b = array.array('i', )
print('Before QuickSort ->', b)
quicksort(b, 'i')
print('After QuickSort ->', b)
Вывод:
Before QuickSort -> array('i', )
After QuickSort -> array('i', )
Транспонирование и изменение формы матриц в numpy
Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием , что отвечает за транспонирование матрицы.

Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать , и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:
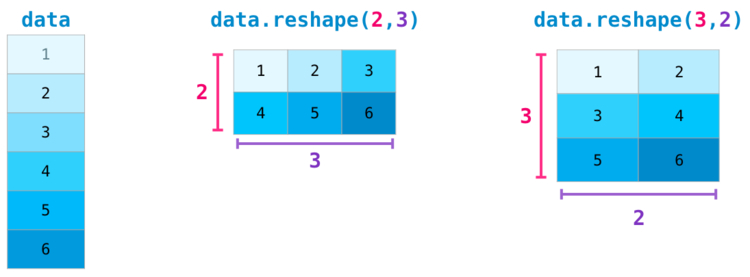
Еще больше размерностей NumPy
NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется , или n-мерным массивом.

В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:

Shell
array(,
,
],
,
,
],
,
,
],
,
,
]])
|
1 |
array(1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1.) |
Добавление нового массива
Перед процессом создание нового массива, необходимо выполнить некоторые действия. Для начала, стоит произвести импорт библиотеки, которая отвечает за работу с подобными объектами. Чтобы выполнить это действие, нужно добавить в файл программы следующую строку: from array import *.
Исходя из того, что массивы предназначены для работы с одним типом данных, то и, соответственно, размер ячеек этих данных также будет одинаков.
Для создания нового массива данных используется такая функция, как «array». Ниже представлен пример того, как заполняется массив с помощью перечисленных действий:
from array import *data = array(‘i’, )
Функция «array» способна принимать два аргумента, одним из них является вид массива, который создается, другим – исходный перечень значений массива. В этом примере i является числом, размер которого составляет 2 б. Стоит отметить, что можно использовать не только этот примитив, но и другие – c, f и т. д.
Действия для добавления нового элемента
Для того, чтобы в массиве появился новый элемент, необходимо воспользоваться таким методом, как «insert». Это делается с помощью ввода в созданный ранее объект двух значений, являющихся аргументами. Цифра 3 представляет собой не что иное, как само значение, а 4 указывает на место в массиве, где будет располагаться элемент, т. е. его индекс.
Действия для удаления нового элемента
В рассматриваемом языке программирования избавиться от лишних элементов можно посредством такого метода, как «pop». Данный метод имеет аргумент (3) и может быть вызван через объект, который создавался ранее, т. е. способом, аналогичным добавлению нового элемента.
data.pop(3)
После того, как произошло удаление лишнего, в массиве происходит сдвиг его содержимого таким образом, чтобы число свободных ячеек памяти совпало с текущим количеством элементов.
Проверка
Зачастую возникает необходимость проверки данных при работе с любой программой, которая проводится путем вывода на экран. Эта операция может быть совершена с помощью такой команды, как «print». Аргументом для этой функции является элемент массива, созданного ранее.
В нижеприведенном примере видно, что обработка массива происходит с помощью цикла «for», в котором любой элемент массива идентификатором i для передачи в «print».
Python NumPy
NumPy IntroNumPy Getting StartedNumPy Creating ArraysNumPy Array IndexingNumPy Array SlicingNumPy Data TypesNumPy Copy vs ViewNumPy Array ShapeNumPy Array ReshapeNumPy Array IteratingNumPy Array JoinNumPy Array SplitNumPy Array SearchNumPy Array SortNumPy Array FilterNumPy Random
Random Intro
Data Distribution
Random Permutation
Seaborn Module
Normal Distribution
Binomial Distribution
Poisson Distribution
Uniform Distribution
Logistic Distribution
Multinomial Distribution
Exponential Distribution
Chi Square Distribution
Rayleigh Distribution
Pareto Distribution
Zipf Distribution
NumPy ufunc
ufunc Intro
ufunc Create Function
ufunc Simple Arithmetic
ufunc Rounding Decimals
ufunc Logs
ufunc Summations
ufunc Products
ufunc Differences
ufunc Finding LCM
ufunc Finding GCD
ufunc Trigonometric
ufunc Hyperbolic
ufunc Set Operations
Python Tutorial
Python HOMEPython IntroPython Get StartedPython SyntaxPython CommentsPython Variables
Python Variables
Variable Names
Assign Multiple Values
Output Variables
Global Variables
Variable Exercises
Python Data TypesPython NumbersPython CastingPython Strings
Python Strings
Slicing Strings
Modify Strings
Concatenate Strings
Format Strings
Escape Characters
String Methods
String Exercises
Python BooleansPython OperatorsPython Lists
Python Lists
Access List Items
Change List Items
Add List Items
Remove List Items
Loop Lists
List Comprehension
Sort Lists
Copy Lists
Join Lists
List Methods
List Exercises
Python Tuples
Python Tuples
Access Tuples
Update Tuples
Unpack Tuples
Loop Tuples
Join Tuples
Tuple Methods
Tuple Exercises
Python Sets
Python Sets
Access Set Items
Add Set Items
Remove Set Items
Loop Sets
Join Sets
Set Methods
Set Exercises
Python Dictionaries
Python Dictionaries
Access Items
Change Items
Add Items
Remove Items
Loop Dictionaries
Copy Dictionaries
Nested Dictionaries
Dictionary Methods
Dictionary Exercise
Python If…ElsePython While LoopsPython For LoopsPython FunctionsPython LambdaPython ArraysPython Classes/ObjectsPython InheritancePython IteratorsPython ScopePython ModulesPython DatesPython MathPython JSONPython RegExPython PIPPython Try…ExceptPython User InputPython String Formatting
Индексирование массивов
Когда ваши данные представлены с помощью массива NumPy, вы можете получить к ним доступ с помощью индексации.
Давайте рассмотрим несколько примеров доступа к данным с помощью индексации.
Одномерное индексирование
Как правило, индексирование работает так же, как вы ожидаете от своего опыта работы с другими языками программирования, такими как Java, C # и C ++.
Например, вы можете получить доступ к элементам с помощью оператора скобок [], указав индекс смещения нуля для значения, которое нужно получить.
При выполнении примера печатаются первое и последнее значения в массиве.
Задание целых чисел, слишком больших для границы массива, приведет к ошибке.
При выполнении примера выводится следующая ошибка:
Одно из ключевых отличий состоит в том, что вы можете использовать отрицательные индексы для извлечения значений, смещенных от конца массива.
Например, индекс -1 относится к последнему элементу в массиве. Индекс -2 возвращает второй последний элемент вплоть до -5 для первого элемента в текущем примере.
При выполнении примера печатаются последний и первый элементы в массиве.
Двумерное индексирование
Индексация двумерных данных аналогична индексации одномерных данных, за исключением того, что для разделения индекса для каждого измерения используется запятая.
Это отличается от языков на основе C, где для каждого измерения используется отдельный оператор скобок.
Например, мы можем получить доступ к первой строке и первому столбцу следующим образом:
При выполнении примера печатается первый элемент в наборе данных.
Если нас интересуют все элементы в первой строке, мы можем оставить индекс второго измерения пустым, например:
Это печатает первый ряд данных.
1.1. Автозаполнение массивов
- Возвращает новый массив заданной формы и типа без инициированных записей.
- Возвращает новый массив с формой и типом данных указанного массива без инициированных записей.
- Возвращает новый массив в котором диагональные элементы равны единице, а все остальные равны нулю.
- Возвращает новый квадратный массив с единицами по главной диагонали.
- Возвращает новый массив заданной формы и типа, заполненный единицами.
- Возвращает новый массив с формой и типом данных указанного массива, заполненный единицами.
- Возвращает новый массив заданной формы и типа, заполненный нулями.
- Возвращает новый массив с формой и типом данных указанного массива, заполненный нулями.
- Возвращает новый массив заданной формы и типа все элементы которого равны указанному значению.
- Возвращает новый массив с формой и типом данных указанного массива, все элементы которого равны указанному значению.
Примеры работы с NumPy
Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.
Математические формулы NumPy
Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу , которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:

Реализовать данную формулу в NumPy довольно легко:

Главное достоинство NumPy в том, что его не заботит, если и содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:

У обоих векторов и по три значения. Это значит, что в данном случае равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:

Затем мы можем возвести значения вектора в квадрат:

Теперь мы вычисляем эти значения:

Таким образом мы получаем значение ошибки некого прогноза и за качество модели.
Представление данных NumPy
Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:
Создание, вывод и ввод матрицы в Питоне
- Таким образом, получается структура из вложенных списков, количество которых определяет количество строк матрицы, а число элементов внутри каждого вложенного списка указывает на количество столбцов в исходной матрице.
Рассмотрим пример матрицы размера 4 х 3:
matrix = -1, , 1,
-1, , 1,
, 1, -1,
1, 1, -1
|
Данный оператор можно записать в одну строку:
matrix = -1, , 1, -1, , 1, , 1, -1, 1, 1, -1 |
Вывод матрицы можно осуществить одним оператором, но такой простой способ не позволяет выполнять какой-то предварительной обработки элементов:
print(matrix) |
Результат:
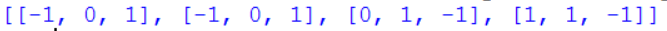
Для вывода матрицы в виде таблицы можно использовать специально заготовленную для этого процедуру:
- способ:
1 2 3 4 5 |
def printMatrix ( matrix ):
for i in range ( len(matrix) ):
for j in range ( len(matrixi) ):
print ( "{:4d}".format(matrixij), end = "" )
print ()
|
В примере i – это номер строки, а j – номер столбца;len(matrix) – число строк в матрице.
способ:
1 2 3 4 5 |
def printMatrix ( matrix ):
for row in matrix:
for x in row:
print ( "{:4d}".format(x), end = "" )
print ()
|
Внешний цикл проходит по строкам матрицы (row), а внутренний цикл проходит по элементам каждой строки (x).
Для инициализации элементов матрицы случайными числами используется алгоритм:
1 2 3 4 5 6 |
import random
for i in range(N):
for j in range(M):
matrixij = random.randint ( 30, 60 )
print ( "{:4d}".format(matrixij), end = "" )
print()
|