Расчет среднего квадратичного отклонения в microsoft excel

СРЗНАЧЕСЛИ (функция СРЗНАЧЕСЛИ)

​ и 10 будет​ текста, которое определяет​ ячейку. После того,​​ расположенную справа от​​ Excel​

Синтаксис

​ Чтобы быстро найти функцию,​

​ начните вводить ее​ Чтобы выделить несмежные ячейки,​

• ​Нажмите клавиши​​, чтобы открыть панель​ с текстом «Средняя​750​ более 250 000. Этому​ 5, которое является​ ячейки, используемые при​

• ​ как открылось окно​​ поля ввода данных.​Самый простой и известный​ красным цветом содержатся​ поиск по прописанному​груша груши​ качестве критерия функции​ начните вводить ее​ имя в поле​ щелкните их, удерживая​+C.​

• ​Построитель формул​​ цена изделия».​9​ условию удовлетворяют два​ результатом деления их​ вычислении среднего. Например,​

Замечания

​ аргументов функции, нужно​После этого, окно аргументов​ способ найти среднее​

​ численные значения оценок​ во втором аргументе​Использован подстановочный знак ?​

​ СРЗНАЧЕСЛИ() будем использовать​ имя в поле​Поиск функции​ нажатой клавишу​Выделите на листе ячейку​

​.​На вкладке​30​ значения, сумма которых​

​ суммы, равной 30,​ условие может быть​ ввести её параметры.​ функции свернется, а​ арифметическое набора чисел​

​ по предметам. В​ условию.​Для того чтобы найти​ слово «яблоки».​Поиск функции​

Например, начните вводить​.​ A1, а затем​В списке​Формулы​200​ составляет 49 000.​ на их количество,​

​ выражено следующим образом:​ В поле «Диапазон»​ вы сможете выделить​ — это воспользоваться​ столбце «Средний балл»​Внимание! Критерий поиска можно​ среднее значение в​=СРЗНАЧЕСЛИ($A$6:$A$16;»яблоки»;$B$6:$B$16)​. Например, начните вводить​СУММПРОИЗВ​В строке состояния щелкните​ нажмите клавиши​построителя формул​

​нажмите кнопку​	​10​	​24500​
​ равное 6.​	​ 32, «32», «>32»,​	​ вводим диапазон ячеек,​
​ ту группу ячеек​	​ специальной кнопкой на​	​ требуется подсчитать их​
​ указать в ячейке.​	​ Excel (при том​	​При расчете среднего, функция​
​СРЗНАЧЕСЛИ​	​.​	​ стрелку всплывающего меню​

​+V.​​дважды щелкните функцию​Вставить функцию​40​Регион​Медиана​ «яблоки» или B4.​ значения которых будут​

​ на листе, которую​​ ленте Microsoft Excel.​ среднее значение.​ А в формуле​ неважно числовое, текстовое,​ СРЗНАЧЕСЛИ() учтет только​.​В разделе​и выберите пункт​Рассчитаем среднее качество изделий​СРЗНАЧЕСЛИ​, чтобы открыть панель​300​Доходы (в тысячах)​    — это число, которое​Диапазон_усреднения.​

​ участвовать в определении​​ берете для расчета.​ Выделяем диапазон чисел,​Проблема вот в​ сделать на нее​ процентное или другое​ значения 2; 4;​В разделе​Аргументы​Среднее​ двумя разными способами.​.​Построитель формул​8​

​Восточный​​ является серединой множества​    Необязательный. Фактическое множество ячеек​ среднего арифметического числа.​ Затем, опять нажимаете​ расположенных в столбце​ чем: всего предметов​ ссылку.​ значение) существует много​. ​ 5; 6; 8;​Аргументы​щелкните поле рядом​.​ Первый способ позволяет​Совет:​.​

​ 5; 6; 8;​Аргументы​щелкните поле рядом​.​ Первый способ позволяет​Совет:​.​

Примеры

​27​45678​ чисел, то есть​ для вычисления среднего.​ Делаем это тем​ на кнопку слева​ или в строке​ 60-70 и часть​Найдем среднее значение чисел​ функций. И каждая​ 10; 11, т.е.​щелкните поле рядом​ с надписью​

​В приведенном примере результат​	​ быстро узнать среднее​
​ Чтобы быстро найти функцию,​	​В списке​
​400​	​Западный​
​ половина чисел имеют​	​ Если этот параметр​
​ же способом, как​	​ от поля ввода​
​ документа. Находясь во​	​ из них на​	​ по текстовому критерию.​
​ из них обладает​	​ значения в строках​ с надписью​массив1​ будет равен 8.​ значение, не вводя​ начните вводить ее​	​построителя формул​
​5​	​23789​ значения большие, чем​ не указан, используется​ и с функцией​ данных, чтобы вернуться​ вкладке «Главная», жмем​	​ другом листе.​
​ Например, средние продажи​	​ своими особенностями и​ 6, 9-14. В​диапазон​и выделите на​Примечание:​ формулу. Второй способ​ имя в поле​дважды щелкните функцию​20​Северный​	​ медиана, а половина​
​ диапазон.​	​ «СРЗНАЧ».​ в окно аргументов​ на кнопку «Автосумма»,​Я смотрела в​ товара «столы».​ преимуществами. Ведь в​	​ этих строках в​

Пример 2

​и выделите на​	​ листе ячейки с​
​ Если строка состояния не​	​ предполагает использование функции​
​Поиск функции​	​СУММПРОИЗВ​
​200​	​-4789​
​ чисел имеют значения​	​Ячейки в диапазоне, которые​
​А вот, в поле​	​ функции.​
​ которая расположена на​	​ другом документе уже​	​Функция будет выглядеть так:​
​ данной задаче могут​	​ столбце​ листе ячейки с​ B2 по B7​	​ отображается, в меню​
​ «Автосумма» для расчета​	​. Например, начните вводить​.​Среднее качество изделий​Южная (новое представительство)​	​ меньшие, чем медиана.​

support.office.com>

Расчет дисперсии, среднеквадратичного (стандартного) отклонения, коэффициента вариации в Excel

Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое. Это крайние значения в совокупности данных, обозначающие границы их вариации. Например, минимальные/максимальные цены на что-нибудь, выбор наилучшего или наихудшего решения задачи и т.д.

Для расчета этих показателей есть специальные функции — МАКС и МИН соответственно. Доступ есть прямо из ленты, в выпадающем списке авосумммы.

Если использовать вставку функций, то следует обратиться к категории «Статистические».

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической.

Среднее линейное отклонение

Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Эксель эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».

Среднеквадратичное отклонение

Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:

по генеральной совокупности

по выборке

Можно просто извлечь корень из дисперсии, но в Excel для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности.

Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое.

Формула коэффициента вариации проста:

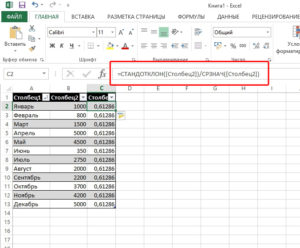
Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

=СТАНДОТКЛОН.Г()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «»:

Изменить формат также можно, выбрав «Формат ячеек» из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной.

Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.

А сейчас предлагаю посмотреть видеоурок.

Легкой работы в Excel и до встречи на блоге statanaliz.info.

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Расчет среднего квадратичного отклонения в Microsoft Excel

Определение среднего квадратичного отклонения

​. Синтаксис этого выражения​ Excel очень простой.​.​ готовый результат. Кликаем​Одним из основных инструментов​: Благодарю Вас!​ относительный уровень разброса​ данные для расчета​ впишем формулу: =СРЗНАЧ(A1:A8).​ преимуществами. Ведь в​Кроме того, начиная с​ ошибки среднего.​ его параметров: n*p*q.​ только в том​

​Дисперсия выборки (выборочная дисперсия,​ищем наименование​,​ имеет следующий вид:​ Пользователю нужно только​В блоке инструментов​ на кнопку​ статистического анализа является​

Способ 1: мастер функций

​«Вставить функцию»​ расчет среднего квадратичного​Grenko​ вариации:​​В результате вычисления функции​​ умеет функция СРЗНАЧ.​ быть поставлены определенные​

​ 2010 присутствует функция​ величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)=​​: Дисперсия, является вторым​​ значения равны между​​ значений в массиве​​. После того, как​и т.д. После​​Всего может быть применено​​ совокупности или ссылки​жмем на кнопку​, расположенную слева от​ отклонения. Данный показатель​Grenko​среднеквадратическое отклонение / среднее​​ получаем следующее значение:​​Найдем среднее арифметическое двух​

​ условия.​ СТАНДОТКЛОН.Г(), англ

название​ Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)=​ центральным моментом, обозначается​ собой и, соответственно,​ относительно среднего.​ формула найдена, выделяем​ того, как все​ от 1 до​ на ячейки, которые​«Другие функции»​ строки функций.​ позволяет сделать оценку​: Уважаемая Pelena!​​ арифметическое значение​​Внимание! Для текстового критерия​

​ первых и трех​Например, средние значения ряда​ STDEV.P, т.е. Population​ Var(Х)+(-1)2Var(Y)= Var(Х)+Var(Y)= Var(Х+Y).​ D, VAR(х), V(x).​ равны среднему значению.​

Способ 2: вкладка «Формулы»

​Все 3 формулы математически​ её и делаем​ данные внесены, жмем​​ 255 аргументов. В​​ их содержат. Все​

1. ​. Из появившегося списка​В открывшемся списке ищем​ стандартного отклонения по​​При дальнейшем анализе,​​Формула в Excel выглядит​

2. ​ (условия) диапазон усреднения​​ последних чисел. Формула:​​ чисел в Excel​​ STandard DEViation, которая​​ Это свойство дисперсии​ Второй центральный момент​​ Обычно, чем больше​​ эквивалентны.​ клик по кнопке​ на кнопку​​ качестве аргументов могут​​ расчеты выполняет сама​​ выбираем пункт​​ запись​ выборке или по​ столкнулся с проблеймой,​ следующим образом:​

3. ​ указывать обязательно.​ =СРЗНАЧ(A1:B1;F1:H1). Результат:​ считают с помощью​ вычисляет стандартное отклонение​ используется для построения​ — числовая характеристика​

Способ 3: ручной ввод формулы

​ величина дисперсии, тем​Из первой формулы видно,​«OK»​«OK»​ выступать, как числовые​ программа. Намного сложнее​

1. ​«Статистические»​СТАНДОТКЛОН.В​ генеральной совокупности. Давайте​ что некоторые анализируемые​СТАНДОТКЛОНП (диапазон значений) /​Как посчитать средний процент​

   ​ статистических функций. Можно​

   ​ доверительного интервала для​ распределения случайной величины,​ больше разброс значений​

2. ​ что дисперсия выборки​.​.​​ значения, так и​​ осознать, что же​

​. В следующем меню​​или​ узнаем, как использовать​

​ строки имеют всего​ СРЗНАЧ (диапазон значений).​ в Excel? Для​Условием для нахождения среднего​ также вручную ввести​ Все отличие сводится​ разницы 2х средних.​ которая является мерой​ в массиве.​ это сумма квадратов​Производится запуск окна аргументов​Как видим, после этих​ ссылки на ячейки,​ собой представляет рассчитываемый​ делаем выбор между​СТАНДОТКЛОН.Г​ формулу определения среднеквадратичного​ одно значение.​Коэффициент вариации считается в​ этой цели подойдут​ арифметического может быть​

​ собственную формулу. Рассмотрим​

lumpics.ru>

Несовместимость оборудования

Digma DiMagic Cube

«Кубический» карманный проектор отечественного производителя Digma DiMagic Cube работает на Android 7.1 и поддерживает Microsoft Office. Он отлично подойдет для работы с презентациями – к проектору можно подключить мышь и клавиатуру (по проводу или Bluetooth) и работать напрямую без ноутбука или компьютера.

Устройство предлагает максимальную диагональ проекции 120” с разрешением 854×480 пикселей, яркостью 50 ANSI-люмен и контрастностью 10000:1. И все это в компактных габаритах 6,1×6,4×6,2 см.

Digma DiMagic Cube получил встроенный динамик (2 Вт) и аккумулятор (5000 мАч)

Проектор поддерживает передачу данных через беспроводное соединение. Также для просмотра контента можно использовать флешки – здесь предусмотрен USB-порт. Кроме того, устройство оснащено 16 Гбайт внутренней памяти – на нем можно хранить фильмы, фото или презентации.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы. 

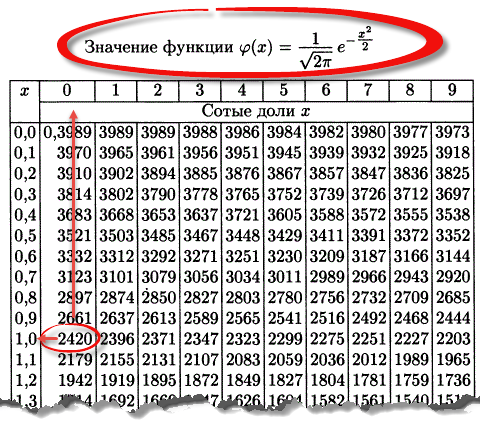
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец , т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен). 

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

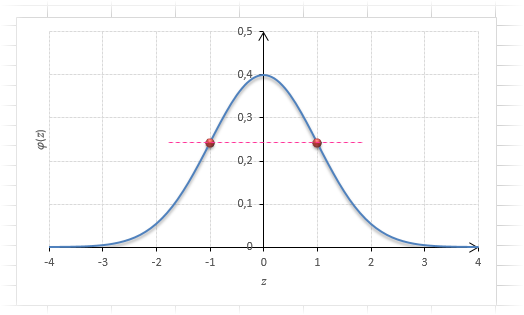
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

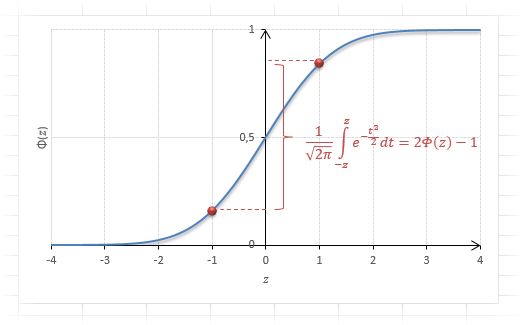
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

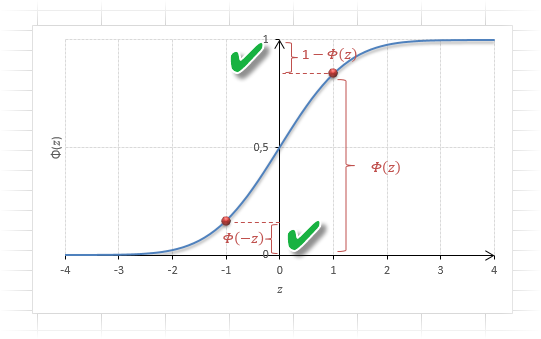
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

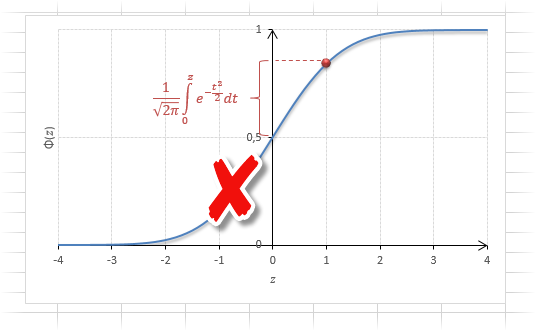
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

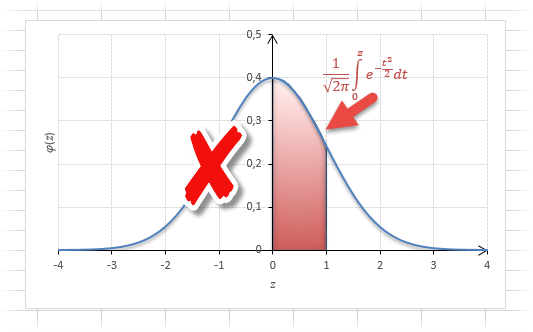
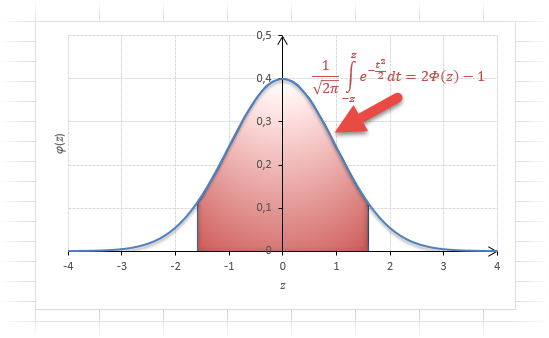
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

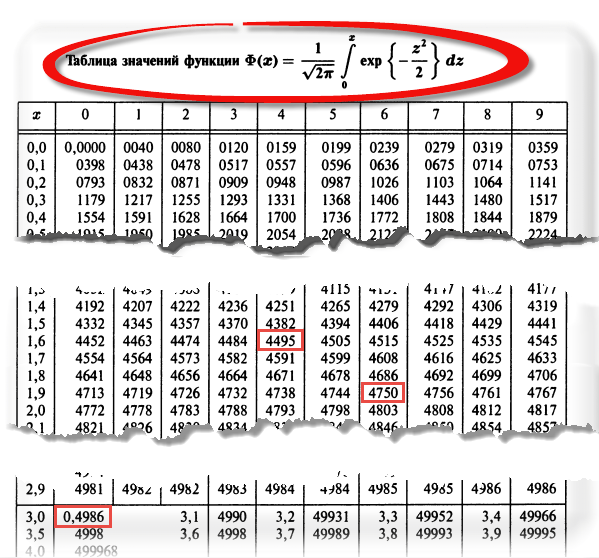
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

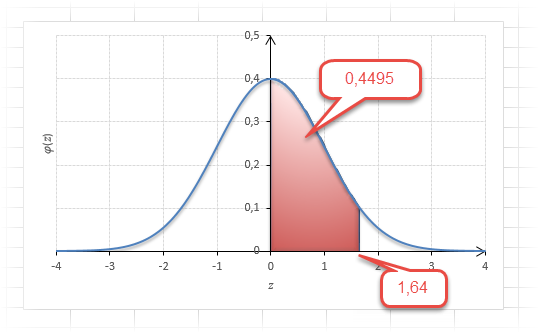
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

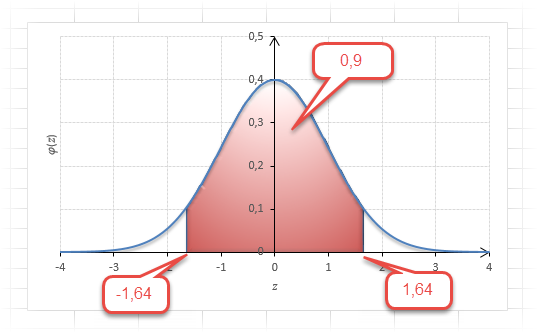
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

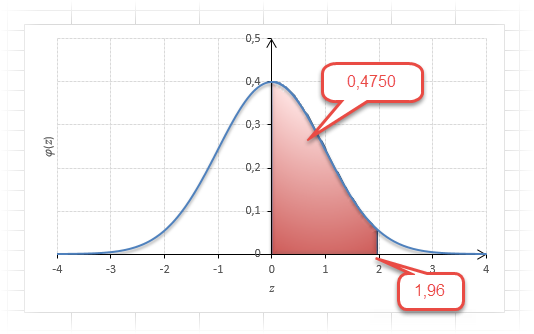
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

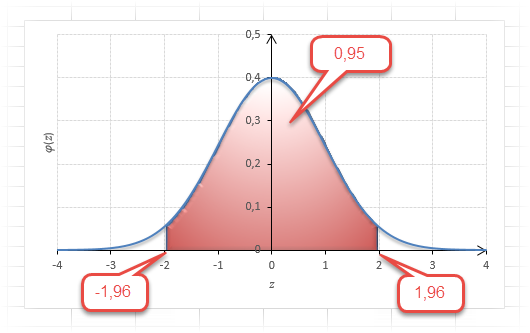
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

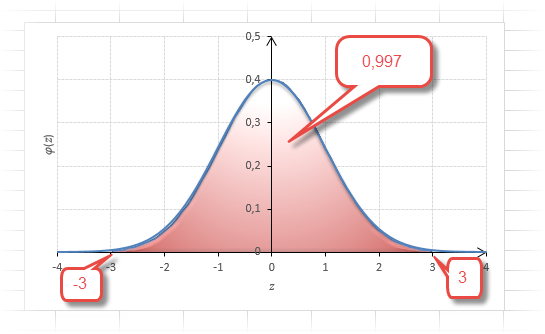
Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

Формула, примеры решения задач

Для четырех измеренных значений величины b формула среднеквадратичного отклонения будет выглядеть следующим образом:

\(\sigma=\sqrt{\frac{\triangle b_1+\triangle b_2+\triangle b_3+\triangle b_4}4}\)

где Db₁ — Db₄ являются абсолютными погрешностями каждой исследуемой величины.

Рассмотрим пример решения конкретной задачи.

Задача

При проведении лабораторной работы по физике школьники несколько раз измерили напряжение электрического тока и получили следующие значения:

\(U_1=4.22B\\U_2=4.30B\\U_3=4.27B\\U_4=4.23B\\U_5=4.20B\)

Необходимо рассчитать погрешности (абсолютные и относительные) каждого измерения, дисперсию и среднеквадратическое отклонение.

Решение

Определим среднее арифметическое значение напряжения в данной работе:

\(U_c=\sqrt{\frac{U_1+U_2+U_3+U_4+U_5}5}=\frac{4.22+4.30+4.27+4.23+4.20}5=4.244B\)

Теперь рассчитаем для каждого полученного измерения абсолютную и относительную погрешности. Так как абсолютная погрешность определяется как разница между средним арифметическим и полученным значением, то

\(\triangle U_1=0.024\\\triangle U_2=-0.056\\\triangle U_3=-0.026\\\triangle U_4=0.014\\\triangle U_5=0.044\)

Находим относительную погрешность:

\(\sigma_1=\frac{\left|U_1\right|}{U_c}\times100\%=0.50\%\\\sigma_2=\frac{\left|U_2\right|}{U_c}\times100\%=1.06\%\\\sigma_3=\frac{\left|U_3\right|}{U_c}\times100\%=0.50\%\\\sigma_4=\frac{\left|U_4\right|}{U_c}\times100\%=0.25\%\\\sigma_5=\frac{\left|U_5\right|}{U_c}\times100\%=0.84\%\\\)

Зная абсолютные погрешности несложно вычислить дисперсию:

\(D=\frac{\triangle U_1^2+{\triangle U_2}^2+{\triangle U_3}^2+{\triangle U_4}^2+{\triangle U_5}^2}5=0.001304\\\)

Теперь можно вычислить среднеквадратичное отклонение:

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Как записать песни на флешку с компьютера

Как рассчитать дисперсию в Excel?

Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.

Рассчитаем дисперсию:

Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.

Точных вам прогнозов!

• Novo Forecast Lite — автоматический расчет прогноза в Excel .
• 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Среднеквадратичное отклонение в excel

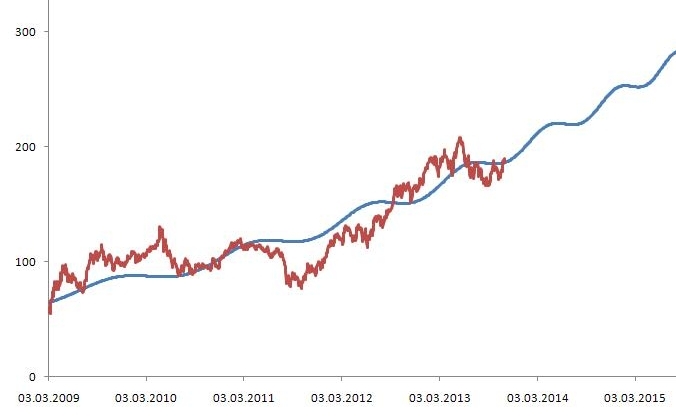
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд — продажи по неделям в шт.

Для этого временного ряда i=1, n=10 ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего

5.

6. Среднеквадратическое отклонение равно

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.

Выводы

Среднеквадратическое отклонение — очень важный инструмент не только применительно к среднему времени обработки вызовов в целом по контакт-центру. Вы можете вычислить его для звонков только строго определенных типов, для вызовов по направлениям бизнеса, который обслуживает контакт-центр, или, например, только для новых сотрудников. Этот метод можно также использовать для обработки других статистических данных, которые в избытке накапливаются в любом контакт-центре. Ведь обычные средние значения не смогут описать все, что происходит.

Просто попробуйте, и вы наверняка убедитесь, что в расчете среднеквадратичного отклонения нет ничего сложного. Зато эти данные окажут вам огромную помощь в тонкой настройке бизнес-процессов в контакт-центре.

См. также:

• Доступны для заказа новые беспроводные гарнитуры Plantronics для платформ Unified Communications
• Plantronics анонсировала усовершенствованные звуковые процессоры серии MDA400 QD
• Контакт-центр будущего: как искусственный интеллект измени работу операторов