Функции для работы с матрицами в excel

Яндекс сколько стоит машина

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

 

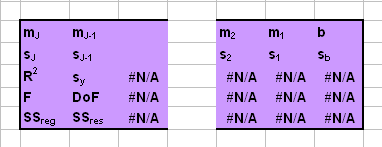
Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Простые операции в Excel: сложение, вычитание

≡  14 Апрель 2016   ·  Рубрика: Могучий MS Excel   

Excel – универсальный инструмент, сложный программный продукт, используемый в различных отраслях.

Но какие-бы сложные инструменты вы не использовали, без простых формул, содержащих элементарные математические операции, вам не обойтись.

Далее я расскажу о том, как делать формулы, содержащие операции сложения и вычитания.

Сложение в Excel – одна из наиболее частых операций, применяемых для создания формул. Рядом со сложением смело можно поставить операцию вычитания. По своему алгебраическому смыслу операции идентичны, но имеют «разный знак». Простейшие алгебраические формулы, которые мы часто видели на школьной доске, выглядят следующим образом.

Простые операции в алгебре

Возможно вы не поверите, но то что вы видели в школе на доске, немногим будет сложнее сделать в Excel. Прежде всего, нужно уяснить, что любая формула в Excel делается по следующим правилам и понятиям:

1. Весь лист разбит на ячейки, и к каждой ячейке можно обратится по адресу. Обычно адрес ячейки выглядит так «А1», «В7». Эти адреса означают, что ячейка находится в столбце А и строке 1 или столбце В и строке 7.
2. Если нужно записать любую формулу, то она записывается в ячейку.
3. В том случае если используются простые операции, тогда, для того, чтобы перейти в режим ввода формулы, нужно поставить знак «=».
4. По завершению ввода формулы нужно нажать «Ввод»
5. В ячейке будет виден результат выполнения формулы, а не сама формула.

Простая операция: сложение, вычитание

Теперь построим формулы сложения и вычитания в Excel.

Допустим: значение А хранится в ячейке «А1», значение В в ячейке В1. В ячейку С1 нужно записать результат суммы А1 и В1, а в ячейке С2 произвести вычитание В1 из А1.

• Формулы сложения и вычитания будут выглядеть так.
• =А1+В1
• =А1-В1

Вид формулы сложения

Вид формулы вычитания

Все четко видно на картинках, хочется только добавить  — не забывайте нажимать Ввод после окончания ввода любой формулы, не обязательно сложения или вычитания. И понятно, что для сложения используется символ «+», для вычитания символ «-».

Сложные варианты сложения: Функция СУММ()

Одним из сложных вариантов является прибавление процентов. Из-за сложности вопроса я написал отдельную статью.

КАК ПРИБАВИТЬ ПРОЦЕНТЫ В EXCEL С ПОМОЩЬЮ ФОРМУЛЫ

Прежде всего, нужно рассмотреть сложение ячеек по столбцу. Наилучший способ использование в формуле функции «СУММ». Этой функции передается диапазон ячеек и/или указываются, через точку с запятой, ячейки, по которым нужно провести суммирование.

Вид задания

Посмотрите на рисунок, условия задачи таковы: в ячейку F6 нужно записать сумму чисел записанных в диапазоне С1:С5, прибавить D1 и прибавить диапазон чисел записанный в D3:D5.

1. Становимся курсором в позицию F6 и нажимаем на кнопку «Вставить функцию».
2. В открывшемся окне «Мастер функций», есть поле поиск функции , в него мы записываем «Сумм»(без кавычек) и нажимаем кнопку «Ок»(в диалоговом окне)!

Мастер функций

После проделанных действий откроется другое диалоговое окно «Аргументы функции».

Теперь для функции сумм нужно установить параметры – диапазоны и ячейки для суммирования

Обращаю внимание, что таких параметров может быть 255 и при ручном вводе разделять их нужно символом «;»

Аргументы функций

После нажатия на кнопке , в ячейке F6 будет записана формула содержащая функцию суммирования, но пользователь увидит результат суммирования.

Думаю, прочитав эту статью, вы убедились, что операции сложения и вычитания это очень просто. Могу лишь посоветовать экспериментировать, экспериментировать и еще …

Метод 2: Использование поэлементного умножения

Так что до сих пор мы разбираем каждую позицию в результирующей матрицеC,найти отдельные элементы, а затем суммировать их вместе. Если вы помните, что-то вроде, Конечно, должен быть другой путь? Что если вместо того, чтобы делать отдельные продукты, а затем суммировать их, мы умножаем векторы за один раз, чтобы получить результирующий вектор, и суммируем полученный вектор, чтобы получить конечный элемент?

m = tensor()n = tensor()m*n>>tensor()

До сих пор мы находили отдельные продуктыи сложить их вместе, Но, действительно, все это можно заменить на:

m = tensor()n = tensor()(m*n).sum()>>tensor(60)

Если вы помните, самый внутренний цикл внаходил отдельные продукты и добавлял их. Ну, мы можем заменить этот цикл, чтобы выполнить векторное поэлементное произведение и положитьв конце концов, и PyTorch / NumPy имеют возможность выполнять поэлементные операции для нас!

Вот как это выглядит в Excel:

C = сумма (A * B )

Точно так же мы получаемпутем умножения вектора в строке 0с вектором на цв 3Ви суммируя полученный вектор.

C = сумма (A * B )

И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.

C = сумма (A * B )

Обратите внимание, как это отличается отМетод-1? На этот раз мы просто говорим Excel или PyTorch: умножьте строку 0с col 0 изВи суммируем полученный вектор, чтобы дать нам ответ. Вместо того чтобы делать, Например, дляэтот метод умножает Vector на строку 0с вектором в столбце 0 изВчтобы получить промежуточный продукт Вектори суммирует это, чтобы дать результат в положениикак,. В коде это выглядит так:

В коде это выглядит так:

def matmul2(a,b):    ar,ac = a.shape    br,bc = b.shape    assert ac==br    c = torch.zeros(ar,bc)    for i in range(ar):        for j in range(bc):            c = (a*b).sum()    return c

Таким образом, мы просто анализируем каждую позициюC,используя две петли FOR и введите соответствующий результат в этой позиции. Еслипредставляют строки и столбцы вСэто выглядит примерно так …

i:0,j:0a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:0,j:1a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:0,j:2a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:0,j:3a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:1,j:0a:tensor(),b:tensor()tensor(,        ,        ,        ])

И так далее .. пока мы не получим полную матрицуС,

tensor(,        ,        ,        ])

Деление в экселе: как применяется, формула, примеры

Microsoft Office Excel имеет в своем наборе огромную библиотеку функций, которые позволяют проводить анализ числовых данных. Однако программа с легкостью может выступать в роли обычного калькулятора. Для этого в формулы с клавиатуры вставляются базовые математические операции и проводятся вычисления. Сегодня подробнее рассмотрим, как проводить деление в экселе.

Формула и примеры, как делить

Чтобы редактор проводил расчеты, необходимо для начала в активной ячейке поставить знак равно, после этого записать выражение. Сейчас разберем, как сделать деление, и рассмотрим основные варианты использования формулы.

Простые числа

В ячейке после знака равно ставите нужные цифры через знак деления, который на клавиатуре обозначается наклонной чертой. Его можно найти в цифровом блоке или справа от буквы ю на английской раскладке. То есть, чтобы в экселе поставить деление в формулу, достаточно нажать одну кнопку на клавиатуре.

На заметку! Можно одновременно использовать несколько операторов. Последовательность вычислений определена математическими законами: сначала умножение и деление, а потом сложение и вычитание.

Формула будет иметь следующий вид:

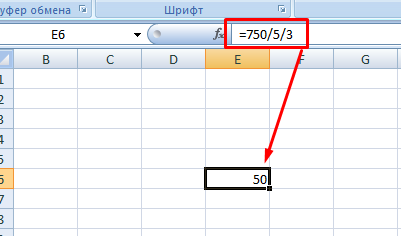
Ссылки на ячейки

Аналогичным образом можно использовать адреса ячеек внутри выражения. Тогда нужно четко указывать числитель и знаменатель.

Можно совмещать два предыдущих способа, если, например, знаменатель является неизменным численным значением.

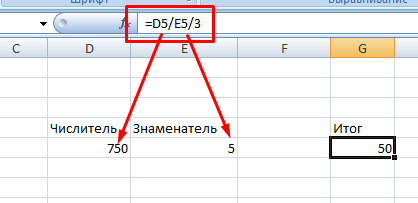
Деление колонки на колонку

Достаточно часто нужно поделить один массив данных на другой. Для этого записываете выражение для одной строки и используете маркер автозаполнения, чтобы формула применялась для всего массива. Например, известна выручка от продажи партии продуктов, а также цена за единицу, необходимо найти количество проданных фруктов.

Решение задачи будет выглядеть следующим образом:

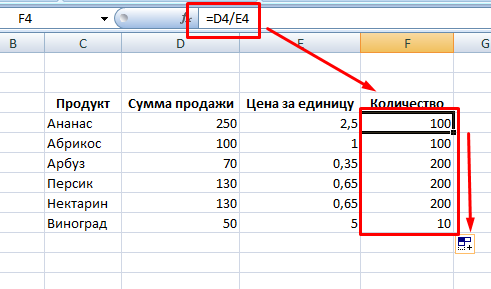
Аналогичным способом выполняется поиск решения, если числитель или знаменатель являются константой. Для этого необходимо зафиксировать значение внутри формулы, то есть сделать абсолютную ссылку на ячейку. Это можно сделать при помощи значка доллара или горячей клавиши F4.

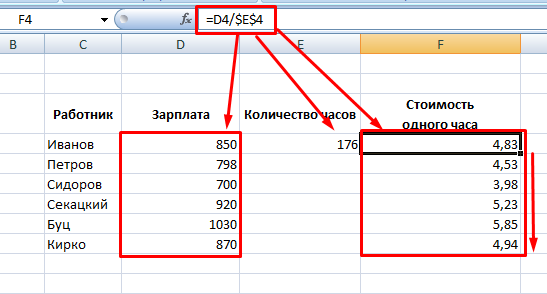
Как известно из математики, провести деление на ноль нельзя. В редакторе также невозможно провести такую операцию. При этом достаточно не только нуля в знаменателе, но и пустой ячейки. Программа выдаст ошибку #ДЕЛ/0.

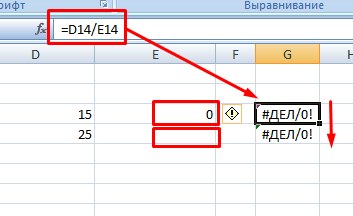
Функция

Помимо использования пользовательской формулы, в excel есть специальная функция, которая выводит результат в виде целых чисел. Она называется ЧАСТНОЕ. Выражение имеет два известных оператора – числитель и знаменатель.

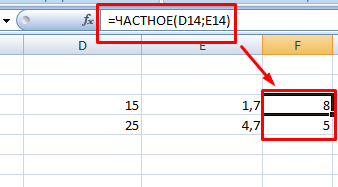
Однако у этой функции есть одна особенность: в процессе работы округление происходит не по правилам математики, то есть после пяти в большую сторону, а до ближайшего целого. Для сравнения проведем операцию деления простейшей формулой.

Этот момент стоит учитывать при использовании данной функции.

Как видите, делить числа в эксель не сложно. Достаточно знать расположение знака деления на клавиатуре и правильно задать формулу. Если же используете специальную функцию, то помните про округление цифр до ближайшего целого.

Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С
будет равен сумме соответствующих элементов матриц А
и В
, т.е. с ij
= а ij
+ b
ij
.

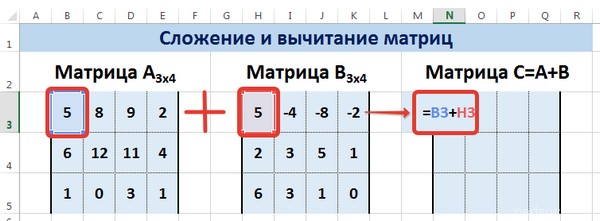
Рассмотрим матрицы А
и В
размерностью 3х4
. Вычислим сумму этих матриц. Для этого в ячейку N
3
введем формулу =B3+H3
, где B3
и H3
— первые элементы матриц А
и В
соответственно. При этом формула содержит относительные ссылки (В3
и H
3
), чтобы при копировании формулы на весь диапазон матрицы С
они могли измениться.

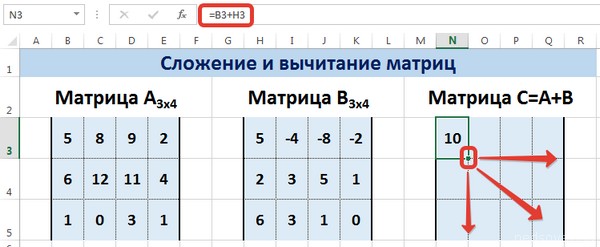
С помощью маркера автозаполнения скопируем формулу из ячейки N
3
вниз и вправо на весь диапазон матрицы С
.

Для вычитания матрицы В
из матрицы А
(С=А — В
) в ячейку N
3
введем формулу =B3 — H3
и скопируем её на весь диапазон матрицы С
.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А
, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В
. После ввода формулы нажимаем сочетание клавиш Ctrl+
Shift+
Enter
, чтобы значениями заполнился весь диапазон.

3 .1. Программирование. Язык VBA

Иногда стандартных возможностей Excel не хватает и приходится
добавлять свои собственные подпрограммы. Для этой цели служит специальный язык
программирования – Microsoft Visual Basic for Applications (VBA)
. С его помощью
можно создавать макросы
– наборы команд, выполняющих определенную
последовательность действий, и функции
– программы для специальных вычислений на
листе. Макросы – это способ автоматизации стандартных процедур. Однажды создав
макрос, его можно использовать для повтора рутинных действий. Обратиться к
макросу можно через меню Tools-Macro-Macros
. Иногда
удобно бывает приписать макрос к новой кнопке на панели инструментов или на
листе.

Функции, созданные пользователем, вызываются также как и
стандартные, встроенные функции – через Formula Bar
.

Для того, чтобы макросы и пользовательские функции были
доступны для применения, нужно установить соответствующий уровень
безопасности через меню Tools-Macro-Security

(Excel 2003)

Рис.39
Выбор уровня безопасности в Excel 2003

В Excel 2007 установка уровня безопасности происходит
через Office Button-
Excel
Options-
Trust Center.

Рис.40
Выбор уровня безопасности в Excel 2007

Если выбран уровень Medium

(2003) или Disable all macros with notification

(2007), то при каждом входе в Excel система будет запрашивать разрешение
на использование макросов. Мы рекомендуем установить уровни так, как
показано на Рис. 39
или Рис. 40
, но не пренебрегать надежным антивирусом
для проверки посторонних файлов Excel.

При начальной установке Excel 2007 возможности работы с
VBA сильно ограничены. Чтобы восстановить их нужно пройти по цепочке
Office Button– Excel Options–Popular
и
включить опцию Show Developer Tab in the Ribbon
.

Как умножить столбец в Excel на число?

Для умножения столбца в Экселе на число можно составить формулу, указав в ней коэффициент умножения, а можно и без всяких формул через меню умножить весь выделенный диапазон значений на любое число.

Если число, на которое будут умножаться ячейки, находится в ячейке таблицы, то ссылку на эту ячейку в формуле нужно будет сделать абсолютной, чтобы она не менялась при применении формулы к другим ячейкам.

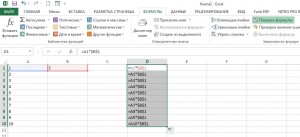
Также в Экселе есть возможность умножения диапазона значений на число с помощью специальной вставки с заменой исходных значений. Для этого нам понадобится скопировать наше число коэффициент в буфер обмена, выделить диапазон ячеек для умножения, и на вкладке «Главная»
в меню «Вставить»
выбрать «Специальная вставка…»
. Или такой же пункт выбрать в меню после нажатия на выделенный диапазон правой кнопкой мыши.

В появившемся окошке в графе «Операция»
выбираем «Умножить»
.

В дальнейшем число коэффициент поменять уже нельзя и все значения останутся неизменными.

В Экселе имеется функция ПРОИЗВЕД
, которая производит перемножение всех указанных в ней аргументов. Обязательный параметр только первый, в котором можно указать диапазон ячеек. Также можно выборочно перечислять ячейки через разделитель точка с запятой.

Как умножать в «Экселе» ячейки между собой?

В наши дни одним из самых популярных средств для сложных вычислений является программа Microsoft Excel. Её широкий функционал позволяет упростить решение множества задач, на которые раньше приходилось тратить немало времени. Сегодня мы рассмотрим, как умножать в «Экселе» ячейки между собой в больших количествах.

Прежде чем разобраться, как умножать в «Экселе» числа, стоит отметить широкую функциональность программы, позволяющей работать как с явным заданием чисел, так и с использованием ячеек, содержащих в себе и сами числа, и формулы, их определяющие. Для того чтобы умножить одну или несколько ячеек на число или другие ячейки, необходимо в строке формул после знака равенства указать данные элементы листа или записать значение самостоятельно.

Далее стоит уяснить принцип, как в «Экселе» умножить ячейку на ячейку и с какими проблемами можно встретиться в процессе. Для перемножения значений двух ячеек необходимо в строке формул прописать следующую конструкцию: «=А*В», где «А» и «В» — ссылки на соответствующие элементы листа «Экселя», то есть ячейки.

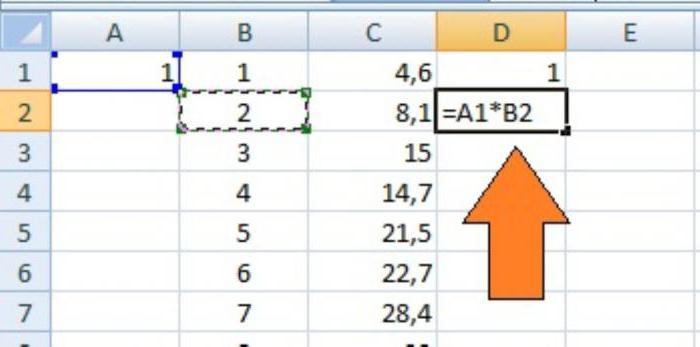
Получив результат, может потребоваться создание его копии, и нередко пользователи, не задумываясь, просто копируют значение этой ячейки, вставляя его в другую. Однако при таком подходе произойдёт изменение и соответствующих ссылок, указывавших на множители. Для того чтобы избежать такой ошибки, следует либо в ячейке, куда необходимо скопировать результат, ввести ссылку на копируемую ячейку, либо «зафиксировать» адрес её множителей с помощью знака «$». Знак доллара сохраняет значение ссылки по параметру, следующему за ним — то есть ссылка $A4 будет всегда относиться к столбцу А, A$4 — к четвертой строке, а $A$4 — только к ячейке А4. Другими словами, фиксация ячейки — создание абсолютной ссылки на неё.

Пользуясь алгоритмом закрепления адреса ячейки, можно перейти непосредственно к тому, как умножить в «Экселе» столбец на столбец или строку на строку. Чтобы не терять время на написание громадной формулы, можно просто воспользоваться свойством изменения ссылки на ячейку при переносе на новый адрес указателя. То есть, если необходимо перемножить попарно значения в двух столбцах, достаточно записать формулу умножения для первой пары ячеек, после чего, удерживая знак «чёрный плюс», появившийся в правом нижнем углу, растянуть результат вниз, вдоль всех значений столбцов-множителей.

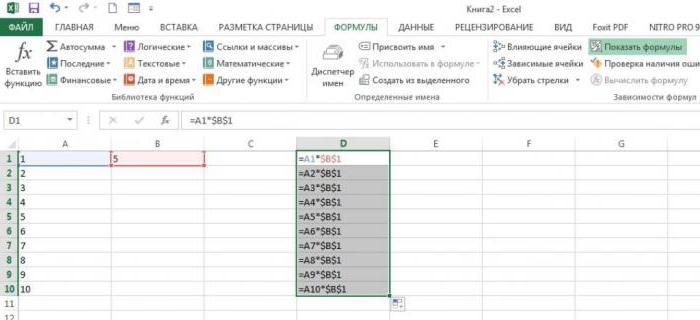
Для того чтобы добиться аналогичного результата для строк, необходимо лишь произвести растягивание результата вдоль соответствующих строк. Стоит отметить: для того чтобы избежать сдвига при дальнейшем копировании результатов, нужно в формуле закрепить указанный столбец или строку — тогда удастся избежать ошибок при вычислении.

Формулы массива в Excel

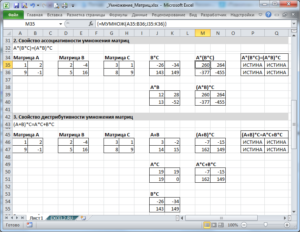
Под массивом обычно понимают набор данных, объединенных в группу. Массивы бывают одномерные (элементы массива образуют строку или столбец) или двумерные (матрица). Легко сообразить, что почти в любой таблице Excel при желании можно найти один или несколько таких массивов:

Формулы массива в Excel – это специальные формулы для обработки данных из таких массивов. Формулы массива делятся на две категории – те, что возвращают одно значение и те, что дают на выходе целый набор (массив) значений. Рассмотрим их на простых примерах…

Пример 1. Классика жанра – товарный чек

Задача: рассчитать общую сумму заказа. Если идти классическим путем, то нужно будет добавить столбец, где перемножить цену и количество, а потом взять сумму по этому столбцу. Если же применить формулу массива, то все будет гораздо красивее:

1. выделяем ячейку С7
2. вводим с клавиатуры =СУММ(
3. выделяем диапазон B2:B5
4. вводим знак умножения (звездочка)
5. выделяем диапазон C2:C5 и закрываем скобку функции СУММ – в итоге должно получиться так:
6. чтобы Excel воспринял нашу формулу как формулу массива жмем не Enter, как обычно, а Ctrl + Shift + Enter

Вуаля!

Т.е. Excel произвел попарное умножение элементов массивов B2:B5 и C2:C5 и образовал новый массив стоимостей (в памяти компьютера), а затем сложил все элементы этого нового массива.

Обратите внимание на фигурные скобки, появившиеся в формуле – отличительный признак формулы массива. Вводить их вручную с клавиатуры бесполезно – они автоматически появляются при нажатии Ctrl + Shift + Enter

Пример 2. Разрешите Вас… транспонировать?

При работе с таблицами часто возникает необходимость поменять местами строки и столбцы, т.е. развернуть таблицу на бок, чтобы данные, которые раньше шли по строке, теперь располагались в столбцах и наоборот. В математике такая операция называется транспонированием. При помощи формулы массива и функции ТРАНСП (TRANSPOSE) это делается на раз.

Допустим, имеем двумерный массив ячеек, который хотим транспонировать.

• Выделяем диапазон ячеек для размещения транспонированной таблицы. Поскольку исходный массив ячеек был 8 строк на 2 столбца, то надо выделить диапазон пустых ячеек размером 2 строки на 8 столбцов.
• вводим функцию транспонирования =ТРАНСП(   
• в качестве аргумента функции выделяем наш массив ячеек A1:B8

жмем Ctrl + Shift + Enter и получаем “перевернутый массив” в качестве результата:

Редактирование формулы массива

Если формула массива расположена не в одной ячейке (как в Примере 1), а в нескольких ячейках (как в Примере 2), то Excel не позволит редактировать или удалить одну отдельно взятую формулу (например в ячейке D10) и выдаст предупреждающее сообщение Невозможно изменить часть массива.

Для редактирования формулы массива необходимо выделить весь диапазон (A10:H11 в нашем случае) и изменить формулу в строке формул (или нажав F2). Затем необходимо повторить ввод измененной формулы массива, нажав сочетание клавиш Ctrl + Shift + Enter.

Excel также не позволит свободно перемещать ячейки, входящие в формулу массива или добавлять новые строки-столбцы-ячейки в диапазон формулы массива (т.е. в диапазон A10:H11 в нашем случае)

Пример 3. Таблица умножения

Вспомните детство, школу, свою тетрадку по математике… На обороте тетради на обложке было что? Таблица умножения вот такого вида:

При помощи формул массива она вся делается в одно движение:

1. выделяем диапазон B2:K11
2. вводим формулу =A2:A11*B1:K1
3. жмем Ctrl + Shift + Enter, чтобы Excel воспринял ее как формулу массива

и получаем результат:

Пример 4. Выборочное суммирование

Посмотрите как при помощи одной формулы массива красиво и легко выбираются данные по определенному товару и заказчику:

 В данном случае формула массива синхронно пробегает по всем элементам диапазонов C3:C21 и B3:B21, проверяя, совпадают ли они с заданными значениями из ячеек G4 и G5. Если совпадения нет, то результат равенства ноль, если совпадение есть, то единица. Таким образом суммы всех сделок, где заказчик не ANTON и товар не Boston Crab Meat умножаются на ноль и суммируются только нужные заказы.

Методы вычисления обратной матрицы

Вычисление обратной матрицы с помощью присоединённой матрицы

Теорема. Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.

Замечание. Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.

Пример 1. Найти обратную матрицу матрицы A

A =		2	4	1
2	1
2	1	1

Решение: Приписываем к матрице A справа единичную матрицу третьего порядка:

A|E =		2	4	1	1		~
2	1	1
2	1	1	1

Преобразуем левую часть полученной матрицы в единичную. Для этого от 3-тей строки отнимем 1-ую строку:

~		2	4	1	1		~
2	1	1
2 — 2	1 — 4	1 — 1	0 — 1	0 — 0	1 — 0

~		2	4	1	1		~
2	1	1
-3	-1	1

Третью строку поделим на (-3) и поменяем местами со второй строкой:

~		2	4	1	1		~
2	1	1
1	1/3	-1/3

~		2	4	1	1		~
1	1/3	-1/3
2	1	1

Отнимем он 1-ой строки 2-ую умноженную на 4; от 3-тей строки 2-ую умноженную на 2:

~		2 — 4·0	4 — 4·1	1 — 4·0	1 — 4·(1/3)	0 — 4·0	0 — 4·(-1/3)		~
1	1/3	-1/3
0 — 2·0	2 — 2·1	1 — 2·0	0 — 2·1/3	1 — 2·0	0 — 2·(-1/3)

~		2	1	-1/3	4/3		~
1	1/3	-1/3
1	-2/3	1	2/3

Отнимем он 1-ой строки 3-ую строку:

~		2 — 0	0 — 0	1 — 1	-1/3 — (-2/3)	0 — 1	4/3 — 2/3		~
1	1/3	-1/3
1	-2/3	1	2/3

~		2	1/3	-1	2/3		~
1	1/3	-1/3
1	-2/3	1	2/3

Разделим 1-ую строку на 2:

~		1	1/6	-1/2	1/3
1	1/3	-1/3
1	-2/3	1	2/3

Ответ: A-1 =		1/6	-1/2	1/3
1/3	-1/3
-2/3	1	2/3

Вычисление обратной матрицы с помощью союзной матрицы

Определение. Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.

A-1 =	1	ÃT
det(A)

Пример 1. Найти обратную матрицу матрицы A

A =		2	4	1
2	1
2	1	1

Решение: Найдем определитель матрицы A:

det(A) =	2	4	1	=
2	1
2	1	1

= 2·2·1 + 4·1·2 + 1·0·1 — 1·2·2 — 2·1·1 — 4·0·1 = 4 + 8 + 0 — 4 — 2 — 0 = 6

Найдем алгебраические дополнения матрицы A:

A11 = (-1)1 + 1·	2	1	= 2·1 — 1·1 = 1
1	1

A12 = (-1)1 + 2·	1	= -(0·1 — 1·2) = 2
2	1

A13 = (-1)1 + 3·	2	= 0·1 — 2·2 = -4
2	1

A21 = (-1)2 + 1·	4	1	= -(4·1 — 1·1) = -3
1	1

A22 = (-1)2 + 2·	2	1	= 2·1 — 1·2 = 0
2	1

A23 = (-1)2 + 3·	2	4	= -(2·1 — 4·2) = 6
2	1

A31 = (-1)3 + 1·	4	1	= 4·1 — 1·2 = 2
2	1

A32 = (-1)3 + 2·	2	1	= -(2·1 — 1·0) = -2
1

A33 = (-1)3 + 3·	2	4	= 2·2 — 4·0 = 4
2

Запишем союзную матрицу:

à =		1	2	-4
-3	6
2	-2	4

Найдем обратную матрицу:

A-1 =  1 ÃT  =  1 det(A) 6

1 -3 2 2 -2 -4 6 4

=

1/6 -1/2 1/3 1/3 -1/3 -2/3 1 2/3

Ответ: A-1 =		1/6	-1/2	1/3
1/3	-1/3
-2/3	1	2/3

Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.

2.9. Виртуальный массив

При анализе данных часто возникает проблема сохранения
промежуточных результатов, которые нужны не сами по себе, а только для
того, чтобы вычислить по ним другие, полезные значения. Например,
остатки в методе PCA часто нам не интересны, а нужны только для
определения полной объясненной дисперсии, ортогональных расстояний и
т.п. При этом размеры таких промежуточных массивов могут быть очень
велики, да и к тому же их приходится вычислять при различных значениях
числа главных компонент. Все это ведет к заполнению рабочей книги
большим количеством ненужных, промежуточных результатов. Этого можно
избежать, если использовать виртуальные массивы. Поясним их суть на
простом примере. 

Рис.38 Пример использования виртуального
массива

Предположим, что задана матрица A, а
нужно вычислить детерминант матрицы AtA
. На Рис. 38 показаны два способа вычисления. Первый – через
последовательность промежуточных массивов, отмеченных красными
стрелками. Второй – с помощью одной формулы, показанной зеленой
стрелкой. Оба пути ведут к одному и тому же результату, но красный путь
занимает на листе много места, а зеленый последовательно использует
несколько промежуточных виртуальных массивов. Все они, по сути,
совпадают с реальными массивами красного пути, но на лист не выводятся.

Первый массив –  это транспонированная матрица At,
получаемая как результат функции
(A).

Второй виртуальный массив получается тогда, когда первый
виртуальный массив умножается на матрицу A с помощью
функции (TRANSPOSE(A), A).  

И, наконец, к этому, второму виртуальному массиву применяется функция
.

Виртуальные массивы очень полезны при вычислении всяческих
вспомогательных характеристик в анализе многомерных данных: остатков,
собственных значений, и т.п. Подробно об этом рассказывается в пособии
Расширение возможностей Chemometrics Add-In.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица