Применение корреляционно-регрессионного анализа

Что стоит знать?

Право на компенсационные выплаты утрачивается, если в последующем ухаживающему лицу назначают другой вид выплат. Либо, если сам инвалид получает официальную работу. Есть и другие основания, позволяющие прекратить перечисления денежных средств:

1. Пенсионера помещают на государственное обеспечение и содержание, в полном объёме.
2. Уход фактически приостановлен, либо прекращён.
3. Умер сам инвалид, либо тот, кто осуществлял уход.
4. Закончился срок назначения той или иной группы инвалидности. Обычно речь идёт о первой.
5. Лишение родительских прав кровных родственников, которые раньше осуществляли уход.

После наступления самого обстоятельства лицо, осуществляющее уход, должно сообщить об этом в территориальное отделение, не позднее, чем через пять дней. Если сообщение не поступает, то орган власти имеет право потребовать компенсации. В том числе, с использованием судебного порядка разрешения споров.

Отдельное заявление подаётся по новому месту жительства, если прежний адрес проживания инвалида был изменён, но фактический уход за ним продолжается. Можно потребовать возмещения сумм, которые не были выплачены ранее. Но максимум они начисляются за три года, которые предшествовали обращению.

Как восстановить доступ к аккаунту

Если пароль к учетной записи Гугл потерян, то рекомендуем воспользоваться сервисом Google Account Recovery. Алгоритм действий следующий:

1. Переходят на страницу услуги. Процедуру удобнее проводить на ПК.
2. В открывшемся окне выбирают диалог «Не помню пароль». Жмут кнопку «Затрудняюсь ответить».
3. Отмечают режим восстановления при помощи сообщения на привязанный телефон. Приходит СМС с цифровым кодом подтверждения.
4. В открывшемся окне вводят комбинацию, жмут ОК.
5. Сервис советует придумать и ввести новый пароль к учетной записи. Изменения сохраняют.

Ссылки

Использование ПО при проведении корреляционного анализа

Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный анализ в Excel предполагает вычисление следующих парамет­ров с использованием функций:

1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ (массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.

Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию ПИРСОН (PEARSON) с теми же массивами.

Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».

После указания исходных данных получаем график.

2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).

3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.

Шесть тысяч четыреста пятьдесят три рубля шестьдесят три копейки

Как вы можете рассчитать корреляцию с помощью Excel? — 2019

a:

Корреляция измеряет линейную зависимость двух переменных. Измеряя и связывая дисперсию каждой переменной, корреляция дает представление о силе взаимосвязи. Или, говоря иначе, корреляция отвечает на вопрос: сколько переменная A (независимая переменная) объясняет переменную B (зависимую переменную)?

Формула корреляции

Корреляция объединяет несколько важных и связанных статистических понятий, а именно дисперсию и стандартное отклонение. Разница — дисперсия переменной вокруг среднего, а стандартное отклонение — квадратный корень дисперсии.

Формула:

Поскольку корреляция требует оценки линейной зависимости двух переменных, то, что действительно необходимо, — это выяснить, какая сумма ковариации этих двух переменных и в какой степени такая ковариация отраженные стандартными отклонениями каждой переменной в отдельности.

Общие ошибки с корреляцией

Самая распространенная ошибка — предполагать, что корреляция, приближающаяся +/- 1, статистически значима. Считывание, приближающееся +/- 1, безусловно увеличивает шансы на фактическую статистическую значимость, но без дальнейшего тестирования это невозможно узнать.

Статистическое тестирование корреляции может усложняться по ряду причин; это совсем не так просто. Критическое предположение о корреляции состоит в том, что переменные независимы и связь между ними является линейной.

Вторая наиболее распространенная ошибка — забыть нормализовать данные в единую единицу. Если вычислять корреляцию по двум бетам, то единицы уже нормализованы: сама бета является единицей

Однако, если вы хотите скорректировать акции, важно, чтобы вы нормализовали их в процентном отношении, а не изменяли цены. Это происходит слишком часто, даже среди профессионалов в области инвестиций

Для корреляции цен на акции вы, по сути, задаете два вопроса: каково возвращение за определенное количество периодов и как этот доход коррелирует с возвратом другой безопасности за тот же период? Это также связано с тем, что корреляция цен на акции затруднена: две ценные бумаги могут иметь высокую корреляцию, если доход составляет ежедневно процентов за последние 52 недели, но низкая корреляция, если доход ежемесячно > изменения за последние 52 недели. Какая из них лучше»? На самом деле нет идеального ответа, и это зависит от цели теста. ( Улучшите свои навыки excel, пройдя курс обучения Excel в Академии Excel. ) Поиск корреляции в Excel

Существует несколько методов расчета корреляции в Excel

Самый простой способ — получить два набора данных и использовать встроенную формулу корреляции:

Это удобный способ расчета корреляции между двумя наборами данных. Но что, если вы хотите создать корреляционную матрицу во множестве наборов данных? Для этого вам нужно использовать плагин анализа данных Excel. Плагин можно найти на вкладке «Данные» в разделе «Анализ».

Выберите таблицу возвратов. В этом случае наши столбцы имеют названия, поэтому мы хотим установить флажок «Ярлыки в первой строке», поэтому Excel знает, как обрабатывать их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.

Как только вы нажмете enter, данные будут автоматически сделаны. Вы можете добавить текст и условное форматирование, чтобы очистить результат.

Для чего нужна подпись

Памятка

1. Корреляция – это соотношение, взаимозависимость нескольких переменных.
2. Связь бывает положительной и отрицательной.
3. Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
4. На основании корреляции люди выдвигают гипотезы (часто ошибочные).
5. Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
6. Бывает ложная корреляционная зависимость.
7. Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Непараметрические методы анализа

Ряд методов позволяет оценить взаимосвязь явлений без количественного выражения признака и, соответственно, параметров распределения. Их называют непараметрическими. Среди них выделяют:

• Коэффициент ранговой корреляции Кендалла (определяет взаимосвязь количественных и качественных значений показателей, в случае если они подлежат ранжированию).
• Коэффициент ранговой корреляции Спирмена (присваивает ранги каждому аргументу и результату, на основе которых определяются разности и вычисляется показатель).
• Коэффициент корреляции знаков Фехнера (определяет количество совпадений и несовпадений отклонений аргументов и результатов от их среднего значения).
• Еще один немаловажный метод корреляционно-регрессионного анализа — Метод наименьших квадратов, позволяющий определить аналитическое выражение взаимосвязи результативного признака и его фактора. Он заключается в построении системы уравнений и определении параметров этих уравнений.

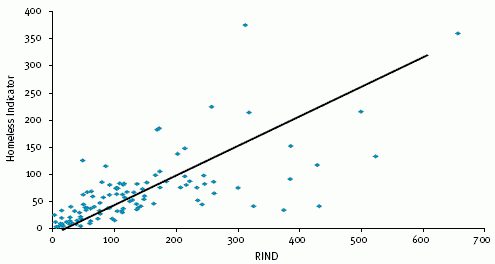
Линейная корреляция Пирсона

Данный коэффициент может использоваться при соблюдении двух условий. Первое – все значения переменных являются рациональными числами, второе – ожидается, что величины изменяются пропорционально. Данный коэффициент всегда находится в пределах между -1 и 1. Если он больше нуля, то имеет место быть прямо пропорциональная зависимость, меньше – обратно, равен – данные величины никак не влияют одна на другую. Умение вычислить данный показатель – это основы корреляционно-регрессионного анализа. Впервые данный коэффициент был разработан Карлом Пирсоном на основе идеи Френсиса Гальтона.

Корреляционный анализ по Спирмену – практическое применение в торговых стратегиях

Корреляционный анализ Спирмена, оценивает рыночную ситуацию с точки зрения ее цикличности, то есть чередования периодов роста и падения. Получается, что трейдеры могут использовать его в торговых стратегиях в качестве определителя трендовых изменений – чем значение коэффициента Спирмена выше, тем больше вероятность того, что произойдет смена тенденции.

Ориентируясь на сигналы индикатора (осциллятора), использующего в своей работе коэффициент Спирмена можно выстроить определенно выгодную торговлю. При этом, значимыми уровнями здесь будут максимальные и минимальные значения, выдаваемые инструментом, которые называются уровнями статистической значимости, как на примере ниже.

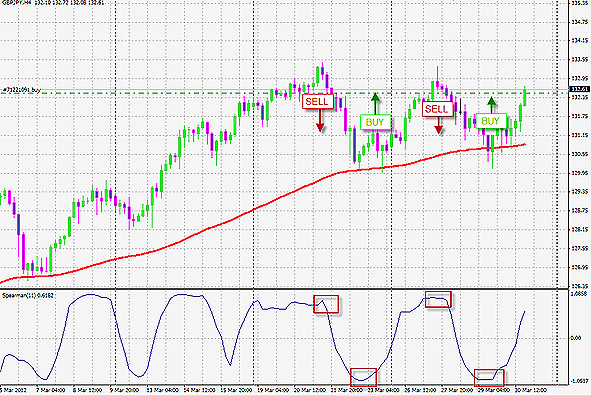
Еще одно практическое применение корреляционный анализ по Спирмену нашел в так называемом парном трейдинге. Называется он так по той причине, что ведется одновременная торговля парами коррелируемых инструментов (опционы, валютные пары, фьючерсные контракты, индексы). То есть парный трейдинг является торговой стратегией основанной на феномене корреляции торговых инструментов.

В свою очередь, различают два вида корреляции в анализе рынка по Спирмену:

• прямая
• и обратная.

На примере ниже мы видим графики прямой или положительной корреляции валютных пар GBP/USD и EUR/USD и отрицательной или обратной корреляции пар USD/CHF и EUR/USD.

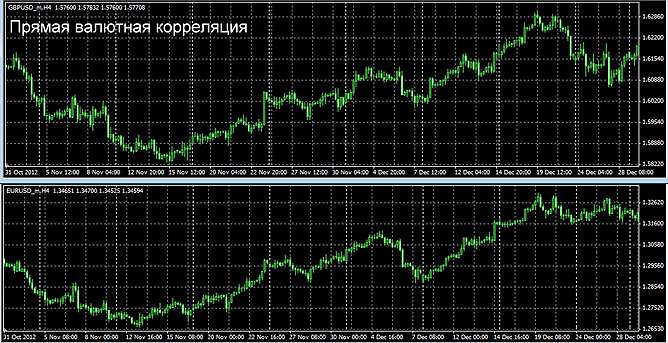
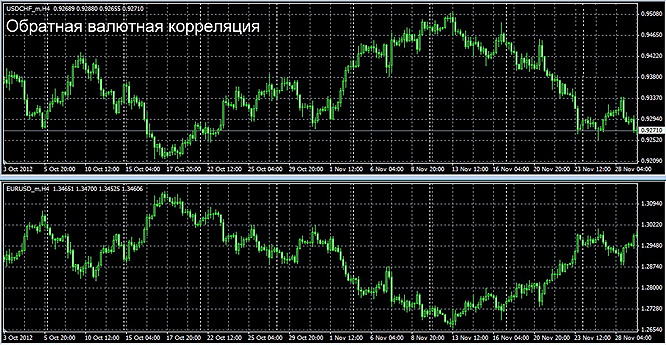
Необходимо отметить, что все пары валют между собой связаны фундаментальными факторами, поэтому примеров их корреляции можно привести очень много, но для парного трейдинга использовать можно не все. Здесь используются лишь те инструменты, степень корреляции которых достаточно высока.

Для подбора таких пар, можно воспользоваться специальными онлайн сервисами, как на примере ниже.

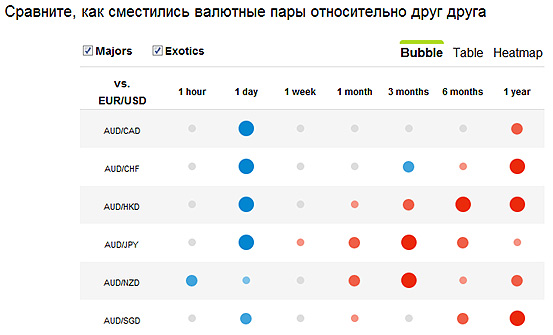
Синими кружками обозначена обратная корреляция, красными – прямая. Теперь давайте рассмотрим, как же происходит торговля по стратегии парного трейдинга, в которой применяется корреляционный анализ по Спирмену.

Первым делом, следует определиться с входом. Вход в сделку необходимо производить лишь убедившись, что коррелируемые пары разошлись по отношению к друг к другу максимально. Чтобы это сделать отмотайте график назад на 6 месяцев и вычислите насколько пунктов было расхождение. После этого определите среднее значение расхождения, по которому будете рассматривать возможный вход.

К примеру, среднее расхождение получилось 80 пунктов, значит рассматривать следует лишь те сделки расхождение между парами которых было как минимум 80 пунктов.

ТОП БРОКЕРОВ, ПРИЗНАННЫХ НЕЗАВИСИМЫМИ РЕЙТИНГАМИ

*БО. Не требуется верификация! | обзор/отзывы | НАЧАТЬ ТОРГОВЛЮ С 10$
*БО. Сделки от 60 рублей. | обзор/отзывы | НАЧАТЬ С 600 ₽

ЛУЧШИЕ ФОРЕКС БРОКЕРЫ ПО ДАННЫМ «ИНТЕРФАКС»

2007 год. FinaCom.   КОПИРОВАТЬ СДЕЛКИ ТРЕЙДЕРОВ | обзор/отзывы
1998 год. FCA, НАУФОР. | +20% ПО КЕШБЭКУ | обзор/отзывы
2007 год. БОНУС $1500 НА СЧЕТ. |
STARTUP BONUS $1500 | обзор/отзывы
2007 год. The FC.   ВЫБЕРИТЕ 10 ИЛИ 20$ НА СЧЕТ | обзор / отзывы

Далее определяемся с правилами входа, а также выхода из позиций. Открываем сразу две позиции, как только расхождение достигает своего максимума – более дорогая валюта (находится сверху) продаем, а более дешевую (снизу), соответственно покупаем. Сразу оговоримся, что в данной стратегии стоп приказы не применяются. Выход осуществляется, когда графики пар валют пересекутся в точке нуля.

Во избежание накапливания размера убытков, если расхождение коррелируемых инструментов будет продолжаться, можно применить локирование.

При этом, если цена начнет двигаться в нужном Вам направлении необходимо вовремя произвести разлокирование позиций.

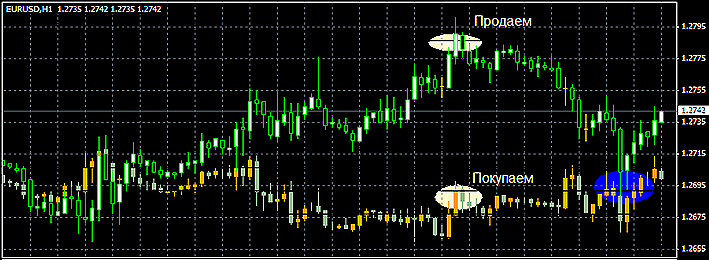
Для данной стратегии в основу которой положен корреляционный анализ, наилучшим образом подходят торговые инструменты имеющие высокую степень корреляции (EUR/USD и GBP/USD, EUR/AUD и EUR/NZD, AUD/USD и NZD/USD, контракты CFD и тому подобные).

Касательно таймфрейма, то рекомендовано выбирать временные промежутки от М5 до Н1, но запомните, что чем выше интервал времени, тем реже появляется сигнал, хотя Take Profit при этом будет больше.

Применение корреляции Спирмена на рынке Форекс

Взаимная корреляция случайных векторов

Определение

Для случайных векторов и , каждый из которых содержит случайные элементы , чьи ожидаемое значение и дисперсию существует, кросс-корреляционная матрица из и определяются
Иксзнак равно(Икс1,…,Иксм)Т{\ Displaystyle \ mathbf {X} = (X_ {1}, \ ldots, X_ {m}) ^ {\ rm {T}}}Yзнак равно(Y1,…,Yп)Т{\ Displaystyle \ mathbf {Y} = (Y_ {1}, \ ldots, Y_ {n}) ^ {\ rm {T}}}Икс{\ displaystyle \ mathbf {X}}Y{\ displaystyle \ mathbf {Y}}

рИксY≜ E⁡ИксYТ{\ displaystyle \ operatorname {R} _ {\ mathbf {X} \ mathbf {Y}} \ треугольник \ \ operatorname {E} }

( Уравнение 3 )

и имеет размеры . Написано покомпонентно:
м×п{\ Displaystyle м \ раз п}

рИксYзнак равноE⁡Икс1Y1E⁡Икс1Y2⋯E⁡Икс1YпE⁡Икс2Y1E⁡Икс2Y2⋯E⁡Икс2Yп⋮⋮⋱⋮E⁡ИксмY1E⁡ИксмY2⋯E⁡ИксмYп{\ displaystyle \ operatorname {R} _ {\ mathbf {X} \ mathbf {Y}} = {\ begin {bmatrix} \ operatorname {E} & \ operatorname {E} & \ cdots & \ operatorname {E} \\\\\ имя оператора {E} & \ operatorname {E} & \ cdots & \ operatorname {E} \\\\\ vdots & \ vdots & \ ddots & \ vdots \\\ \\ operatorname {E} & \ operatorname {E} & \ cdots & \ operatorname {E} \ end {bmatrix}}}

Случайные векторы и не обязательно должны иметь одинаковую размерность, и любой из них может быть скалярным значением.
Икс{\ displaystyle \ mathbf {X}}Y{\ displaystyle \ mathbf {Y}}

пример

Например, если и являются случайными векторами, то
это матрица, -я запись которой равна .
Иксзнак равно(Икс1,Икс2,Икс3)Т{\ displaystyle \ mathbf {X} = \ left (X_ {1}, X_ {2}, X_ {3} \ right) ^ {\ rm {T}}}Yзнак равно(Y1,Y2)Т{\ displaystyle \ mathbf {Y} = \ left (Y_ {1}, Y_ {2} \ right) ^ {\ rm {T}}}рИксY{\ displaystyle \ operatorname {R} _ {\ mathbf {X} \ mathbf {Y}}}3×2{\ displaystyle 3 \ times 2}(я,j){\ displaystyle (я, j)}E⁡ИксяYj{\ displaystyle \ operatorname {E} }

Определение сложных случайных векторов

Если и являются комплексными случайными векторами , каждый из которых содержит случайные величины, ожидаемое значение и дисперсия которых существуют, матрица взаимной корреляции и определяется как
Zзнак равно(Z1,…,Zм)Т{\ Displaystyle \ mathbf {Z} = (Z_ {1}, \ ldots, Z_ {m}) ^ {\ rm {T}}}Wзнак равно(W1,…,Wп)Т{\ Displaystyle \ mathbf {W} = (W_ {1}, \ ldots, W_ {n}) ^ {\ rm {T}}}Z{\ displaystyle \ mathbf {Z}}W{\ displaystyle \ mathbf {W}}

рZW≜ E⁡ZWЧАС{\ displaystyle \ operatorname {R} _ {\ mathbf {Z} \ mathbf {W}} \ треугольник \ \ operatorname {E} }

где обозначает эрмитово транспонирование .
ЧАС{\ displaystyle {} ^ {\ rm {H}}}

Резюме

Особенность киви состоит в том, что данная платежная система не требует при регистрации паспортные данные или какие-либо документы, подтверждающие личность владельца аккаунта. Это предоставляет клиентам платежки возможность оставаться анонимами при выполнении тех или иных переводов, но в этом случае у вас минимальные лимиты в системе. При этом разработана разносторонняя система защиты денежных средств пользователей. Те, кого анонимность не привлекает, могут идентифицировать свою страницу и таким образом увеличить лимит.

Пользователей платежной системы не может не радовать отсутствие комиссии на многие операции и широкий спектр возможностей, который открывается перед участниками программы Qiwi.

 566 

Множественная корреляция, её коэффициент

Множественная корреляция — это вероятностная зависимость между одной величиной с
одной стороны, и одновременно несколькими другими ,
с другой стороны.
То есть, в отличие от парной корреляции, при которой
на изменения зависимой (результирующей) переменной влияет одна независимая (объясняющая) переменная,
при множественной корреляции независимых (объясняющих) переменных две или больше.

Цель корреляционного анализа в случае множественной корреляции — установить, есть ли зависимость между
переменными и насколько тесно связаны между собой зависимая переменная, с одной стороны, и независимые
переменные, с другой стороны, и зависят ли друг от друга независимые переменные .

Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе
множественной корреляции должны быть установлены следующие факты:

• зависимая переменная тесно зависит от независимых переменных (тесноту связи, как и в случае
  парной корреляции, показывают );
• нет тесной зависимости между независимыми переменными.

Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:

.

Коэффициенты множественной корреляции между зависимой переменной
и независимыми переменными
записываются в корреляционную матрицу:

Пример 1. Аналитик предприятия решил проверить факторы, которые
влияют на размер заработной платы сотрудников . Предварительно
в качестве объясняющих факторов выбраны: возраст сотрудника ,
стаж работы , оценка теста для приёма
на работу и число подчинённых
сотрудников . Случайно были выбраны
200 сотрудников, данные которых были обобщены. В результате была получена следующая корреляционная матрица:

	1
	-0,27	1
	0,78	-0,63	1
	-0,83	0,47	-0,89	1
	0,65	-0,46	0,17	-0,21	1

Установить, какие переменные можно выбрать как независимые, для того, чтобы далее
можно было бы строить модель множественной регрессии.

Решение.

Корреляционная матрица показывает, что между переменными:

• и — слабая линейная связь: -0,27;
• и — средне тесная положительная линейная связь: 0,78;
• и — тесная отрицательная линейная связь: -0,83;
• и — средне тесная линейная связь: 0,65;
• и — тесная отрицательная линейная связь: -0,89;
• и — слабая линейная связь: 0,17;
• и — слабая линейная связь: -0,21.

Таким образом, не следует включать в число переменных, влияющих на размер заработной
платы возраст сотрудников . Так как
между независимыми переменными и
установлена тесная отрицательная связь,
не включаем в число переменных, влияющих на размер заработной платы стаж работы .
Выбираем в качестве независимых переменных оценку теста для приёма
на работу и число подчинённых
сотрудников .

Чтобы установить тесноту связи между заработной платой сотрудников ,
с одной стороны, и оценкой теста для приёма
на работу и числом подчинённых
сотрудников , с другой стороны,
вычислим коэффициент множественной (двухфакторной) корреляции:

Таким образом, между заработной платой сотрудников, с одной стороны, и
оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная
связь.

Как показывает пример выше, в исследованиях поведения человека,
как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на
результат при учете влияния всех остальных факторов

Литература

• Гмурман В. Е.<span title=»Статья «Гмурман, Владимир Ефимович» в русском разделе отсутствует»>ru</span>_uk. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
• Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.
• Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
• Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А. А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

Регрессия бывает:

• линейной (у = а + bx);
• параболической (y = a + bx + cx2);
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

У = а + а₁х₁ +…+а_кх_к.

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Hard Reset средствами самой системы Android

Коэффициент корреляции в Excel: что это, как рассчитать? Формула, пример, анализ данных онлайн

Выделяют 2 вида связи между ними:

• функциональная;
• корреляционная.

Корреляция в переводе на русский язык – не что иное, как связь. В случае корреляционной связи прослеживается соответствие нескольких значений одного признака нескольким значениям другого признака. В качестве примеров можно рассмотреть установленные корреляционные связи между:

• длиной лап, шеи, клюва у таких птиц как цапли, журавли, аисты;
• показателями температуры тела и частоты сердечных сокращений.

Для большинства медико-биологических процессов статистически доказано присутствие этого типа связи.

Статистические методы позволяют установить факт существования взаимозависимости признаков. Использование для этого специальных расчетов приводит к установлению коэффициентов корреляции (меры связанности).

Такие расчеты получили название корреляционного анализа. Он проводится для подтверждения зависимости друг от друга 2-х переменных (случайных величин), которая выражается коэффициентом корреляции.

Использование корреляционного метода позволяет решить несколько задач:

• выявить наличие взаимосвязи между анализируемыми параметрами;
• знание о наличии корреляционной связи позволяет решать проблемы прогнозирования. Так, существует реальная возможность предсказывать поведение параметра на основе анализа поведения другого коррелирующего параметра;
• проведение классификации на основе подбора независимых друг от друга признаков.

Для переменных величин:

• относящихся к порядковой шкале, рассчитывается коэффициент Спирмена;
• относящихся к интервальной шкале – коэффициент Пирсона.

Это наиболее часто используемые параметры, кроме них есть и другие.

Значение коэффициента может выражаться как положительным, так и отрицательными.

В первом случае при увеличении значения одной переменной наблюдается увеличение второй. При отрицательном коэффициенте – закономерность обратная.

Для чего нужен коэффициент корреляции?

Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.

Случайные величины, связанные между собой, могут иметь совершенно разную природу этой связи.

Не обязательно она будет функциональной, случай, когда прослеживается прямая зависимость между величинами.

Этапы анализа

Корреляционно-регрессионный анализ экономических процессов разделяется на несколько этапов:

1. Определение аргументов и предварительная обработка условной информации.
2. Определение тесноты и формы взаимосвязи между несколькими признаками.
3. Моделирование представленного экономического процесса и анализ полученной модели.
4. Применение конечных результатов для усовершенствования планирования и менеджмента модели.

Статистическую однородность информации можно определить с помощью двух приемов. Для начала необходимо определить и откинуть значение факторов, резко отличающихся от всех величин. Потом осуществляется статистическое исследование однородности с помощью проверки независимости выборки и ее принадлежности к единственной совокупности с нормальным распределением.

Модель регрессии определяется через метод наименьших квадратов, благодаря которому обеспечивается самое лучшее приближение оценки результата, определенного через уравнение регрессии, к его факторам.