Вычисление обратной матрицы в microsoft excel

По данным портала ЗАЧЕСТНЫЙБИЗНЕСМУНИЦИПАЛЬНОЕ КАЗЕННОЕ УЧРЕЖДЕНИЕ «УПРАВЛЕНИЕ КАПИТАЛЬНОГО СТРОИТЕЛЬСТВА МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН»По данным портала ЗАЧЕСТНЫЙБИЗНЕС2327013058

О компании:
МКУ «УКС МОБР» ИНН 2327013058, ОГРН 1132363000175 зарегистрировано 12.03.2013 в регионе Краснодарский Край по адресу: 352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211. Статус: Действующее. Размер Уставного Капитала — руб.

Руководителем организации является: Начальник — Бандуров Виталий Григорьевич, ИНН . У организации 1 Учредитель. Основным направлением деятельности является «деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях».

Рейтинг организации:
Высокий
  подробнее

ВНИМАНИЕ: для оценки рисков работы с данной организацией рекомендуем отчет

Должная осмотрительность ?

Статус: ?
Действующее

Дата регистрации: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

12.03.2013
Размещенные вакансии

ОГРН  ?	1132363000175    присвоен: 12.03.2013
ИНН  ?	2327013058
КПП  ?	232701001
ОКПО  ?	10122371
ОКТМО  ?	03610407101

Реквизиты для договора 
?
 …Скачать

Проверить блокировку cчетов 
?

Контактная информация +7(8… Посмотреть
?

Отзывы об организации 
?: 0   Написать отзыв

Юридический адрес: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211
получен 04.03.2016
зарегистрировано по данному адресу:
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Руководитель Юридического Лица ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
НачальникПо данным портала ЗАЧЕСТНЫЙБИЗНЕС

Бандуров Виталий Григорьевич

ИНН ?	По данным портала ЗАЧЕСТНЫЙБИЗНЕС
действует с	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 09.06.2018

Учредители ? ()

По данным портала ЗАЧЕСТНЫЙБИЗНЕС По данным портала ЗАЧЕСТНЫЙБИЗНЕС АДМИНИСТРАЦИЯ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН По данным портала ЗАЧЕСТНЫЙБИЗНЕС 12.03.2013 , ИНН

Основной вид деятельности: ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
71.1 деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях

Дополнительные виды деятельности:

Единый Реестр Проверок (Ген. Прокуратуры РФ) ?

Реестр недобросовестных поставщиков: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

не числится.

Реестр операторов, осуществляющих обработку персональных данных (Данные РКН) ?

Регистрационный номер:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 23-16-006129 от По данным портала ЗАЧЕСТНЫЙБИЗНЕС 17.10.2016
Дата начала обработки:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 25.02.2013

Налоговый орган ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Межрайонная Инспекция Федеральной Налоговой Службы № 4 По Краснодарскому Краю
Дата постановки на учет: По данным портала ЗАЧЕСТНЫЙБИЗНЕС
12.03.2013

Регистрация во внебюджетных фондах

Фонд	Рег. номер	Дата регистрации
ПФР  ?	033029023103	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 21.03.2013
ФСС  ?	231242287123121	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 14.03.2013

Коды статистики

ОКАТО  ?	03210807001
ОКОГУ  ?	4210007
ОКОПФ  ?	75404
ОКФС  ?	14

Финансовая отчетность МКУ «УКС МОБР» ?

В качестве Поставщика: , на сумму

В качестве Заказчика: , на сумму

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Судебные дела МКУ «УКС МОБР» ?

найдено по ИНН: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

найдено по наименованию (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Исполнительные производства МКУ «УКС МОБР»
?

найдено по наименованию и адресу (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Лента изменений МКУ «УКС МОБР»
?

Не является участником проекта ЗАЧЕСТНЫЙБИЗНЕС ?

Больше информации об организации — в Премиум доступе

Умножение и деление матрицы на число в Excel

Способ 1

Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

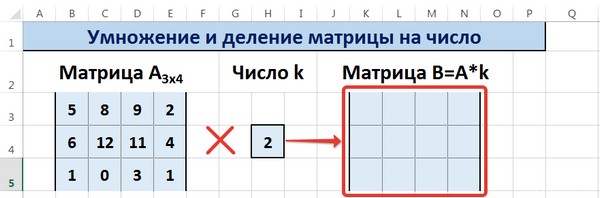
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

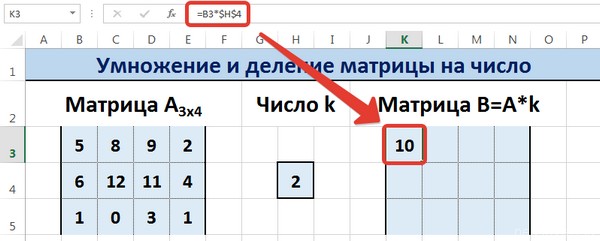
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

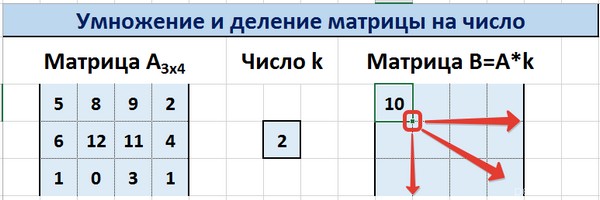
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

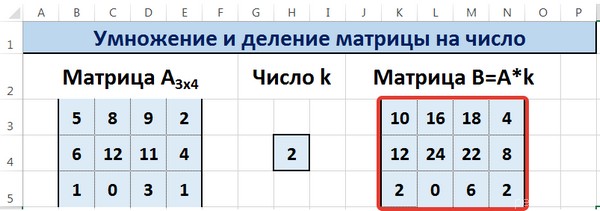
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

 

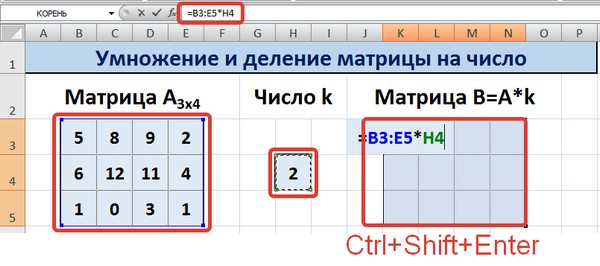
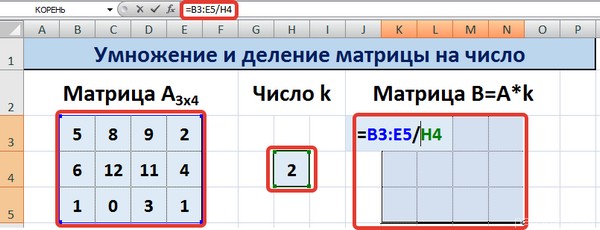
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

Функции массивов

Наиболее удобно в качестве формул использовать уже готовые встроенные функции Excel. Доступ к ним можно получить через Мастер функций, нажав кнопку «Вставить функцию» слева от строки формул. Или же во вкладке «Формулы» на ленте можно выбрать одну из категорий, в которой находится интересующий вас оператор.

После того, как пользователь в Мастере функций или на ленте инструментов выберет наименование конкретного оператора, откроется окно аргументов функции, куда можно вводить исходные данные для расчета.

Правила ввода и редактирования функций, если они выводят результат сразу в несколько ячеек, те же самые, что и для обычных формул массива. То есть, после ввода значения обязательно нужно установить курсор в строку формул и набрать сочетание клавиш Ctrl+Shift+Enter.

Урок: Мастер функций в Excel

Оператор СУММ

Одной из наиболее востребованных функций в Экселе является СУММ. Её можно применять, как для суммирования содержимого отдельных ячеек, так и для нахождения суммы целых массивов. Синтаксис этого оператора для массивов выглядит следующим образом:

Данный оператор выводит результат в одну ячейку, а поэтому для того, чтобы произвести подсчет, после внесения вводных данных достаточно нажать кнопку «OK» в окне аргументов функции или клавишу Enter, если ввод выполнялся вручную.

Урок: Как посчитать сумму в Экселе

Оператор ТРАНСП

Функция ТРАНСП является типичным оператором массивов. Она позволяет переворачивать таблицы или матрицы, то есть, менять строки и столбцы местами. При этом она использует исключительно вывод результата в диапазон ячеек, поэтому после введения данного оператора обязательно нужно применять сочетание Ctrl+Shift+Enter. Также нужно отметить, что перед введением самого выражения нужно выделить на листе область, у которой количество ячеек в столбце будет равно числу ячеек в строке исходной таблицы (матрицы) и, наоборот, количество ячеек в строке должно равняться их числу в столбце исходника. Синтаксис оператора следующий:

Урок: Транспонирование матриц в Excel

Урок: Как перевернуть таблицу в Экселе

Оператор МОБР

Функция МОБР позволяет производить вычисление обратной матрицы. Все правила ввода значений у этого оператора точно такие же, как и у предыдущего

Но важно знать, что вычисление обратной матрицы возможно исключительно в том случае, если она содержит равное количество строк и столбцов, и если её определитель не равен нулю. Если применять данную функцию к области с разным количеством строк и столбцов, то вместо корректного результата на выходе отобразится значение «#ЗНАЧ!»

Синтаксис у этой формулы такой:

Для того чтобы рассчитать определитель, применяется функция со следующим синтаксисом:

Урок: Обратная матрица в Excel

Как видим, операции с диапазонами помогают сэкономить время при вычислениях, а также свободное пространство листа, ведь не нужно дополнительно суммировать данные, которые объединены в диапазон, для последующей работы с ними. Все это выполняется «на лету». А для преобразования таблиц и матриц только функции массивов и подходят, так как обычные формулы не в силах справиться с подобными задачами. Но в то же время нужно учесть, что к подобным выражениям применяются дополнительные правила ввода и редактирования.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Способ 1: Специализированные приложения

Существует довольно много программ, предоставляющих возможность скрытия папок и файлов, а также их защиты путем установки кодовой комбинации. Воспользуемся одним из них для решения нашей сегодняшней задачи.

1. Скачайте приложение с официального сайта, воспользовавшись представленной выше ссылкой. Установите его на свой компьютер и запустите. Придумайте и дважды введите пароль, который будет использоваться для защиты непосредственно Wise Folder Hider.

2. В главном окне перейдите во вкладку «Зашифровать файл» и нажмите по расположенной внизу кнопке «Создать».

Определите параметры создаваемого файла, который на деле будет представлять собой виртуальный диск для хранения данных. Задайте ему имя, укажите папку расположения, выберите размер (в бесплатной версии – не более 50 Мб, но для текстового документа этого более чем достаточно), затем нажмите «Создать».

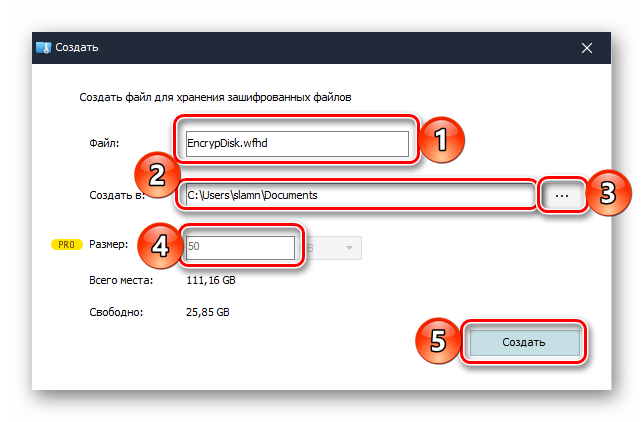
Спустя несколько секунд в окне программы появится созданный виртуальный файл, параллельно с этим в «Проводнике» будет открыто его расположение. Именно в эту директорию и следует поместить документ Word, который вы хотите защитить паролем. Скопируйте и вставьте его сюда или переместите из изначальной папки.

Далее в колонке «Операция» нажмите на указывающий вниз треугольник, чтобы вызвать выпадающий список, и выберите пункт «Установить пароль».

Дважды введите кодовое выражение, которое хотите использовать для защиты текстового файла Ворд и содержащего его виртуального диска. Нажмите «ОК» для подтверждения,

а затем еще раз, чтобы «Задать пароль».

В дальнейшем открыть созданную с помощью Wise Folder Hider папку можно будет через «Этот компьютер», где она отображается в виде одного из накопителей.

Если же в этом перечне диск будет отсутствовать, его потребуется добавить через интерфейс самой программы. В уже знакомой нам колонке «Операция» следует нажать по кнопке «Монтировать», ввести установленный на предыдущем шаге пароль и кликнуть «ОК» для подтверждения. Повторное нажатие кнопки (когда она называется «Размонтировать») скроет накопитель из «Проводника».

Как уже было сказано выше, рассмотренный нами Wise Folder Hider – далеко не единственное программное средство для установки защитной комбинации на папки и файлы. К тому же большинство из них предоставляют еще одни вариант решения нашей сегодняшней задачи – вместо шифрования файла и создания виртуального диска можно поместить требующие защиты данные в отдельную директорию и поставить пароль на нее.

Подробнее:Программы для защиты файлов и папокКак поставить пароль на папку в Windows

Изменение содержимого массива

Новички нередко сталкиваются с трудностями в попытках изменить часть массива, потому что каким бы способом они не пытались бы выкрутиться, Эксель все равно показывает сообщение, что это сделать нельзя. Тем не менее, все гениальное просто. В этом случае – также. Достаточно просто выполнить несколько элементарных действий:

1. Найти кнопку «Отмена», расположенную слева от строки формул. Еще один вариант – нажатие клавиши Esc, которая выполняет ту же операцию. Во всех случаях блокировка будет снята и все операции можно выполнять заново. 
2. Снова ввести формулу массива с тем же диапазоном.

Таким образом, изменение содержимого массива возможно лишь если все отменить, а потом заново вводить формулу. Неудобно, конечно, но значительно удобнее, чем использовать стандартные формулы.

1.10. Построение графиков

В Excel можно строить диаграммы разных типов. Но для нас
интересны только два вида: диаграмма рассеяния (scatter) и  график (line).
Пример диаграммы рассеяния приведен на Рис. 24 .

Рис.24
Диаграмма рассеяния

Диаграммы такого типа используются для построения графиков
счетов, зависимостей «измерено-предсказано», и т.п. От линейных графиков
они отличаются равноправием обеих осей. В линейных графиках ось абсцисс
предназначена только для отображения категорийных переменных, т.е.
величин, в которых важна не их величина, а порядок следования. Поэтому
линейные графики подходят для представления зависимостей от числа
главных компонент, например, для изображения того, как величины RMSEC и
RMSEP меняются при усложнении модели.

Методы построения  графиков в версиях 2003 и 2007 сильно
отличаются. Поэтому мы не будем на этом останавливаться, предоставив эту
тему для

самостоятельного изучения.

Нахождение обратной матрицы методом линейных преобразований

Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице
соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот,
системе линейных уравнений соответствует некоторая матрица.

Поэтому существует метод линейных преобразований для нахождения обратной матрицы.
Для решения задач нам будет достаточно знать, что линейное преобразование — это система линейных
уравнений, вид которой будет приведён ниже в алгоритме.

Алгоритм нахождения обратной матрицы методом линейных преобразований

1. Для данной невырожденной матрицы A составить линейное преобразование —
систему линейных уравнений вида

,

где — элементы
матрицы A.

2. Решить полученную систему относительно y — найти для предыдущего
линейного преобразование обратное линейное преобразование

,

в котором —
алгебраические дополнения элементов матрицы A, Δ — определитель матрицы A

Внимание!
Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки —
в столбце, а для элементов столбца — в строке

3. Находим коэффициенты при y: ,
которые и будут элементами матрицы, обратной для матрицы A.

4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.

Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований —
это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для
кого-то метод линейных преобразований может оказаться более удобным как более компактный.

Пример 4. Найти обратную матрицу для матрицы

.

Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю,
следовательно, обратная матрица существует.

Для данной матрицы записываем линейное преобразование:

.

Находим линейное преобразование, обратное предыдущему, для этого потребуется
находить алгебраические дополнения (урок откроется в новом окне).
Запишем обратное линейное преобразование:

Коэффициенты при иксах в обратном линейном преобразовании — это элементы обратной матрицы
для матрицы A. Таким образом нашли обратную матрицу:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

,  (2)

где —
определитель матрицы А, а

— матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Её определитель:

Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица

того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу
,
транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:

Следовательно, матрица
,
союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Синтаксис формулы массива

Давайте представим, что у нас есть таблица, в которой есть набор ячеек, а сумма к оплате описывается в одной ячейке. Для первого будем искать промежуточные итоги. Во втором же случае будем рассчитывать итоговую сумму.

Для начала нам нужно выделить диапазон, к какому в дальнейшем будет применена формула. В нашем случае это набор ячеек, начинающийся E3, а заканчивающийся E8.

Затем ставим курсор в строку формул, и там записываем =C3:C8*D3:D8.

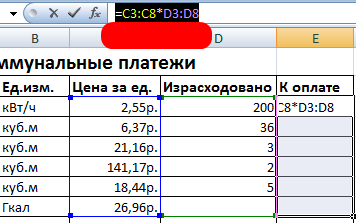3

Превращаем формулу в формат массива. Нужно нажать Ctrl + Shift + Enter.

После этого мы получаем таблицу с готовыми промежуточными итогами.

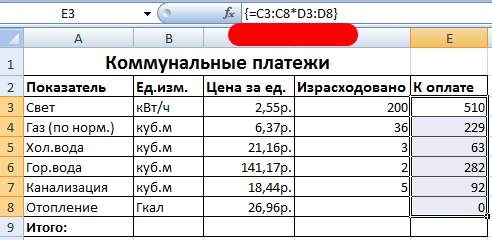4

Как видим, после совершения этих операций формула облачилась в фигурные скобки. Именно они и говорят о том, что эта функция будет обрабатываться, как формула массива. Видим, что каждая ячейка каждого ряда превратилась в готовый результат. 

Если попробовать внести какие-угодно изменения в результирующую ячейку, то появится такое уведомление о том, что операция запрещена.

5

Давайте приведем еще один вариант использования формулы массива. На этот раз мы выведем только одно результирующее значение в итоговую ячейку. Чтобы достичь этой цели, необходимо выполнить следующие действия.

1. Выделяем ту ячейку, которая будет содержать результат вычисления по формуле массива.
2. Вводим туда формулу. В нашем случае мы будем суммировать значения из целевого диапазона, поэтому используем формулу СУММ(C3:C8*D3:D8).
3. С использованием комбинации Ctrl + Shift + Enter осуществляем трансформацию стандартной формулы в ту, которая работает с массивами данных.

По итогу, получаем следующий результат.

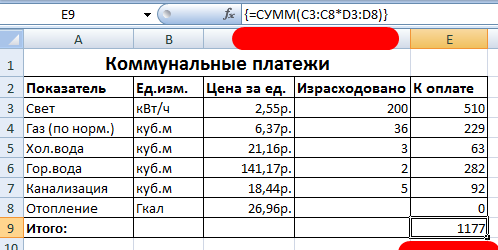6

В случае, если бы мы не знали, как правильно использовать формулы массива, нам бы пришлось использовать две обычные. А так мы избавлены от этой необходимости. 

Давайте более подробно рассмотрим синтаксис этой формулы. 

В нашем случае были использованы одномерные массивы. Формула обрабатывает каждый, после чего выполняет необходимые результаты, а итог выводит в ячейку.

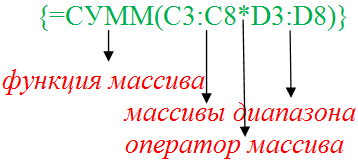
Составные части формул массива:

1. Функция массива. Это описание той операции, которую Эксель должен выполнить. 
2. Массивы диапазона. Это непосредственно те диапазоны, которые будут обрабатываться формулой. 
3. Оператор массива – знак двоеточия. Обозначает расстояние в определенное количество ячеек между конкретными адресами. 

Чтобы было проще понять, вот небольшой рисунок.

7

1.9. «Растаскивание» формул

При работе с данными в виде матрицы, часто возникает
необходимость ввести не одну, а целую серию формул. Например, при
выполнении SNV преобразования спектральных данных нужно вычислить
средние значения и среднеквадратичные отклонения по каждой строке. Очень
утомительно было бы повторять одну и ту же формулу многократно, меняя в
ней только аргумент, даже для сильно усеченного примера, показанного на
. А в реальных данных число строк или
столбцов может доходить до десятков тысяч. К счастью это и не нужно,
поскольку можно воспользоваться техникой «растаскивания» формул. 

Поясним эту технику на нашем примере. Начнем с ввода
формулы-образца. В этом случае –  это формула, помещенная в ячейку
J3  .

 

Рис.21
Маркер заполнения

Формулы в соседние ячейки можно вставить при помощи
маркера заполнения, которым называется небольшой черный квадрат в правом
нижнем углу выделенной области ячеек. При наведении мышки на этот
маркер, указатель принимает вид черного креста. После этого можно
перетащить ячейку, содержащую формулу, в примыкающий диапазон. Тащить
можно по вертикали, как показано на Рис. 22, и по горизонтали.

Рис.22 Растаскивание серии однотипных формул

Формулы можно размножать и другим способом. Сначала
копируем ячейку, содержащую формулу-образец. Потом отмечаем диапазон
ячеек, в которые нужно распространить формулу, и делаем специальную
вставку, выбирая опцию Formulas.

Рис.23
Копирование серии однотипных формул

Отметим, что независимо от способа, ссылки получаются
правильными – на соответствующий диапазон ячеек. Это произошло потому,
что в исходной формуле мы использовали относительную адресацию в
аргументе: B3:I3.

Подробности можно прочитать

здесь. 

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица