Пузырьковая сортировка (сортировка “пузырьком”)

Как создать пузырьковую сортировку

Вот что нам придется делать для создания пузырьковой сортировки:

• Создать два цикла , чтобы проходить по всем элементам массива раз ( это размер массива).
• Сравнивать ячейки массива, с помощью оператора ветвления .
• Менять местами значения ячеек.

В примере ниже мы предложили пользователю заполнить массив, который мы дальше отсортируем используя пузырьковую сортировку.

#include <iostream>

using namespace std;

int main() {
setlocale(LC_ALL, «rus»);

int digitals; // объявили массив на 10 ячеек

cout << «Введите 10 чисел для заполнения массива: » << endl;

for (int i = 0; i < 10; i++) {
cin >> digitals; // «читаем» элементы в массив
}

for (int i = 0; i < 10; i++) {
for (int j = 0; j < 9; j++) {
if (digitals > digitals) {
int b = digitals; // создали дополнительную переменную
digitals = digitals; // меняем местами
digitals = b; // значения элементов
}
}
}

cout << «Массив в отсортированном виде: «;

for (int i = 0; i < 10; i++) {
cout << digitals << » «; // выводим элементы массива
}
system(«pause»);
return 0;
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

#include <iostream>   usingnamespacestd; intmain(){ setlocale(LC_ALL,»rus»); intdigitals10;// объявили массив на 10 ячеек cout<<«Введите 10 чисел для заполнения массива: «<<endl; for(inti=;i<10;i++){ cin>>digitalsi;// «читаем» элементы в массив } for(inti=;i<10;i++){ for(intj=;j<9;j++){ if(digitalsj>digitalsj+1){ intb=digitalsj;// создали дополнительную переменную digitalsj=digitalsj+1;// меняем местами digitalsj+1=b;// значения элементов } } } cout<<«Массив в отсортированном виде: «; for(inti=;i<10;i++){ cout<<digitalsi<<» «;// выводим элементы массива } system(«pause»); return; }

Давайте поподробнее разберем строки 16 — 24 (здесь находится пузырьковая сортировка)

1. В строке 16: мы создали первый цикл .
2. В строке 17: аналогично был создан второй, но уже вложенный цикл.
3. В строке 18: происходит сравнивание двух элементов.
   • Если  результат этого условия положительный, то мы меняем значение элементов.
   • Если же результат отрицателен, то мы пропускаем этап смены значений.
4. В строке 19: создали переменную , чтобы менять значения ячеек и местами.

Давайте посмотрим, что выведет программа выше при запуске:

sort_puzerek.cpp

Введите 10 чисел для заполнения массива:
5 3 6 2 7 0 2 8 9 10

Массив в отсортированном виде: 0 2 2 3 5 6 7 8 9 10
Process returned 0 (0x0) execution time : 0.005 s
Press any key to continue.

Алгоритмы сортировки на собеседовании

Алгоритмов сортировки достаточно много, и вряд ли можно встретить программиста, который может по памяти написать реализацию хотя бы половины из них.

На самом деле, программисты просто гуглят необходимую реализацию. Конечно, они имеют представление о принципах их работы, потому что в своё время рассмотрели несколько алгоритмов, как, например, сортировка пузырьком.

Кроме того, в Python и других языках программирования существуют встроенные функции, которые производят сортировку быстро и эффективно.

На собеседованиях спрашивают про алгоритмы сортировки, но это не значит, что от будущего работника требуют написать их реализацию или придумать свой. Работодатель требует от специалиста следующее:

• Уметь классифицировать алгоритмы сортировки.
• Знать преимущества и недостатки популярных алгоритмов, чтобы понимать, когда каждый из них лучше использовать.
• Понимать, что такое сложность алгоритма и как с её помощью определять, подходит ли он для решения данной задачи.

Быстрая сортировка (Quick Sort)

Этот широко известный алгоритм сортировки был разработан английским информатиком Чарльзом Хоаром во время его работы в МГУ в советские годы.

Один из самых быстрых известных универсальных алгоритмов сортировки массивов: в среднем O(n log n) обменов при упорядочении n-элементов; из-за наличия ряда недостатков на практике обычно используется с некоторыми доработками.

Быстрая сортировка относится к алгоритмам «разделяй и властвуй».

Алгоритм состоит из трёх шагов:

1. Выбор опорного элемента из массива.
2. Перераспределение элементов в массиве таким образом, что элементы меньше опорного помещаются перед ним, а больше или равные — после.
3. Рекурсивное применение первых двух шагов к двум подмассивам слева и справа от опорного элемента. Рекурсия не применяется к массиву, в котором только один или отсутствуют элементы.

С исходным кодом алгоритма и его интерактивной презентацией вы сможете ознакомиться на специальном ресурсе.

Таблица 2: Сортировка пузырьком в многопоточном режиме

1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
2	1	3	4	5	6	7	8	9	10	11	12	13	14
2	3	1	4	5	6	7	8	9	10	11	12	13	14
3	2	4	1	5	6	7	8	9	10	11	12	13	14
3	4	2	5	1	6	7	8	9	10	11	12	13	14
4	3	5	2	6	1	7	8	9	10	11	12	13	14
4	5	3	6	2	7	1	8	9	10	11	12	13	14
5	4	6	3	7	2	8	1	9	10	11	12	13	14
5	6	4	7	3	8	2	9	1	10	11	12	13	14
6	5	7	4	8	3	9	2	10	1	11	12	13	14
6	7	5	8	4	9	3	10	2	11	1	12	13	14
7	6	8	5	9	4	10	3	11	2	12	1	13	14
7	8	6	9	5	10	4	11	3	12	2	13	1	14
8	7	9	6	10	5	11	4	12	3	13	2	14	1
8	9	7	10	6	11	5	12	4	13	3	14	2	1
9	8	10	7	11	6	12	5	13	4	14	3	2	1
9	10	8	11	7	12	6	13	5	14	4	3	2	1
10	9	11	8	12	7	13	6	14	5	4	3	2	1
10	11	9	12	8	13	7	14	6	5	4	3	2	1
11	10	12	9	13	8	14	7	6	5	4	3	2	1
11	12	10	13	9	14	8	7	6	5	4	3	2	1
12	11	13	10	14	9	8	7	6	5	4	3	2	1
12	13	11	14	10	9	8	7	6	5	4	3	2	1
13	12	14	11	10	9	8	7	6	5	4	3	2	1
13	14	12	11	10	9	8	7	6	5	4	3	2	1
14	13	12	11	10	9	8	7	6	5	4	3	2	1
14	13	12	11	10	9	8	7	6	5	4	3	2	1

Сложность алгоритма

Сложность алгоритма позволяет дать ему оценку по времени выполнения, то есть определяет его эффективность.  Можно выражать сложность по-разному, но чаще всего используется асимптотическая сложность, которая определяет его эффективность при стремлении входных данных к бесконечности.

Точное время выполнения алгоритма не рассматривается, потому что оно зависит слишком от многих факторов: мощность процессора, тип данных массива, используемый язык программирования.

Алгоритм сортировки пузырьком имеет сложность , где – количество элементов массива. Из формулы видно, что сложность сортировки пузырьком квадратично зависит от количества сортируемых элементов. Это значит, что он неэффективен при работе с большими массивами данных.

Следует понимать, что с помощью асимптотической функции нельзя точно вычислить время работы алгоритма. Например, дана последовательность “6 5 4 3 2 1”, для её сортировки придется сделать максимальное количество проходов. Такой случай называют наихудшим. Если дана последовательность “3 1 2 4 5”, то количество проходов будет минимально, соответственно сортировка пройдет гораздо быстрее. Если же дан уже отсортированный массив, то алгоритму сортировки и вовсе не нужно совершать проходов. Это называется наилучшим случаем.

2. Обзор алгоритмов сортировки

Сортировка — это процесс перестановки объектов данного множества в определённом порядке. Цель сортировки — облегчить последующий поиск элементов в отсортированном множестве. Поэтому элементы сортировки присутствуют во многих задачах прикладного программирования.

Рассмотрим алгоритмы сортировки «на месте», то есть те алгоритмы в которых не используется копирование массива.

Удобной мерой эффективности алгоритмов сортировки «на месте» является число необходимых сравнений в ходе сортировки и число необходимых пересылок элементов.

Эффективные алгоритмы сортировки требуют порядка

сравнений, где N — число элементов, а С — число необходимых сравнений.

Мы рассмотрим простые методы сортировки, которые требуют число сравнений порядка

Методы сортировки «на месте» можно разбить на три основных класса:

сортировка выбором

сортировка вставками

сортировка обменом

В сортировке выбором выбирается элемент с наибольшим значением ключа и меняется местами с последним. Затем то же самое повторяется для s-1 элемента. Найденный элемент с наибольшим значением ключа меняется

Рисунок 1. Сортировка простым выбором

В сортировке включениями элементы разделяются на уже упорядоченную и неупорядоченную последовательности. В начале упорядоченная часть содержит только один элемент. Очередной элемент из начала неупорядоченной части вставляется на подходящее место в упорядоченную часть. При этом упорядоченная часть удлиняется на один элемент, а неупорядоченная — укорачивается. Сортировка заканчивается при исчезновении неупорядоченной части (рисунок 2).

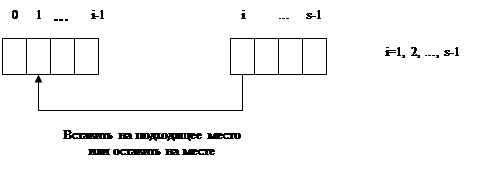
Рисунок 2. Сортировка простыми включениями

Основная характеристика сортировки обменом — перестановка местами двух соседних элементов, если они расположены не так, как требует отсортированный массив.

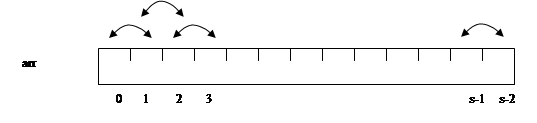
Рисунок 3. Сортировка простым обменом

В рассмотренной классификации существуют разные алгоритмы. Они отличаются сложностью, быстротой выполнения, последовательностью операций.

Например:

сортировка вставками;

пузырьковая сортировка;

корневая сортировка;

пирамидальная сортировка;

сортировка слиянием;

быстрая сортировка;

сортировка Шелла и др.

Рассмотрим подробнее основные типы и виды сортировок (сначала простые сортировки затем более сложные).

Сортировка массива простым выбором

Метод основан на следующем правиле:

Выбирается элемент с наибольшим значением ключа

Он меняется местами с последним элементом arr . Затем эти операции повторяются с оставшимися первыми s-1 элементами, затем — с s-2 первыми элементами и т.д. до тех пор, пока не останется только первый элемент — наименьший. Пример сортировки методом простого выбора показан на рисунке 4:

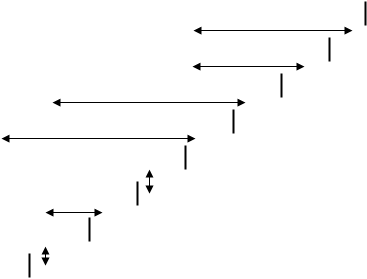
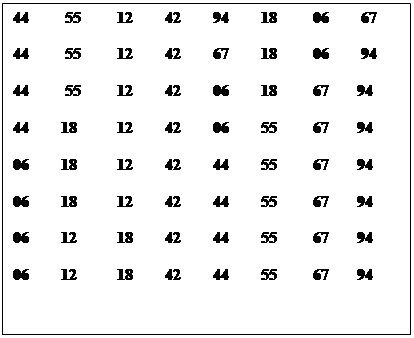
Рисунок 4. Сортировка массива простым выбором

Эффективность сортировки простым выбором. Число сравнений ключей не зависит от начального порядка ключей. Операция сравнения выполняется в теле цикла с управляющей переменной k

и средним числом повторений size/2. Этот цикл, в свою очередь, находится в теле цикла с управляющей переменной L

и числом повторений size −1. Таким образом, число сравнений

С= (size −1) * size −1/2

Число пересылок, напротив, зависит от начального порядка ключей. Если принять, что операция сравнения в теле цикла по k

дает результат «истина» в половине случаев, то среднее число пересылок в этом цикле равно size/4. Цикл по L

, как указывалось выше, выполняется size −1 раз и в теле цикла выполняется три пересылки и цикл по k

. С учетом этого число пересылок:

М= (3+ size/4) * (size −1)

Получаем, что при сортировке простым выбором и число сравнений, и число пересылок пропорционально .

2.1 Сортировка массива простыми включениями

Метод простых вставок предполагает разделение всего массива элементов на упорядоченную часть, которая вначале содержит лишь один элемент, и неупорядоченную. Очередной элемент из неупорядоченной части вставляется в определенное место упорядоченной части, проходя сравнение с ее элементами. При поиске подходящего места удобно чередовать сравнения и пересылки, т.е. как бы «просеивать» выбранный элемент, сравнивая его с очередным элементом a и либо вставляя, либо пересылая a направо и продвигаясь налево. Заметим, что «просеивание» может закончиться при двух различных условиях: найден элемент a с ключом меньшим, чем ключ x или достигнут левый конец готовой последовательности.

При этом упорядоченная часть удлиняется на один элемент. Сортировка заканчивается при окончании неупорядоченной части.

При данной сортировке общее число сравнений приблизительно равно

,

При этом требуется количество проходов по данным P

Рисунок 5. Пример сортировки массива простыми включениями

Число Ci сравнений ключей при i-м просеивании составляет самое большее i-1, самое меньшее 1 и, если предположить, что все перестановки n ключей равновероятны, в среднем равно i/2. Число Мi пересылок (присваиваний) равно Ci+2 (учитывая барьер). Поэтому общее число сравнений и пересылок есть

Cmin = n-1 Mmin = 2 (n-1)

Cср. = (n2+n-2) /4 Mср. = (n2+9n-10) /4

Cmax = ( (n2+n) — 1) /2 Mmax = (n2+3n-4) /2.

Алгоритм сортировки простыми включениями можно легко улучшить, пользуясь тем, что готовая последовательность a ,…, a , в которую нужно включить новый элемент, уже упорядочена. Поэтому место включения можно найти значительно быстрее, применив бинарный поиск, который исследует средний элемент готовой последовательности и продолжает деление пополам, пока не будет найдено место включения.

Анализ

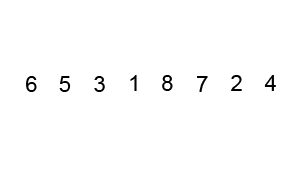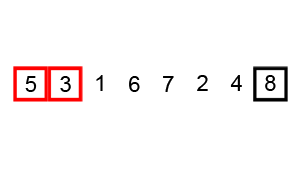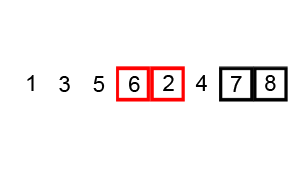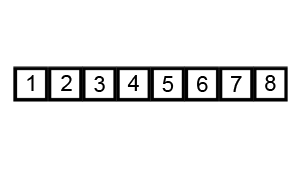
Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации нужно сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.

Производительность

Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n  log  n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.

Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь свой процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (с небольшим количеством инверсий ).

В случае больших коллекций следует избегать пузырьковой сортировки. Это не будет эффективно в случае коллекции с обратным порядком.

Кролики и черепахи

Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен переместиться в конец списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается с начала. С другой стороны, элемент, который должен двигаться к началу списка, не может перемещаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n -1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .

Были предприняты различные усилия по устранению черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Комбинированная сортировка сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам для сглаживания списка. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .

Пошаговый пример

Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему с помощью пузырьковой сортировки. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;

Первый проход

( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.

(1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4

(1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2

(1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже в порядке (8> 5), алгоритм не меняет их местами.

Второй проход

( 1 4 2 5 8) → ( 1 4 2 5 8)

(1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритм нужен один весь проход без какой — либо свопа знать сортируется.

Третий проход

( 1 2 4 5 8) → ( 1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Использовать

Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя

Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение.

Хотя пузырьковая сортировка является одним из самых простых алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках, состоящих из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.

Из-за своей простоты пузырьковая сортировка часто используется для знакомства с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.

Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковой сортировке, похоже, нечего рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.

Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в ​​худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.

Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .

В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.

Как улучшить пузырьковую сортировку

Ниже вы можете видеть оптимизированную версию пузырьковой сортировки.

for (int i = 0; i < 10; i++) {
bool flag = true;
for (int j = 0; j < 10 — (i + 1); j++) {
if (digitals > digitals) {
flag = false;
swap (digitals, digitals);
}
}
if (flag) {
break;
}
}

1 2 3 4 5 6 7 8 9 10 11 12

for(inti=;i<10;i++){ boolflag=true; for(intj=;j<10-(i+1);j++){ if(digitalsj>digitalsj+1){ flag=false; swap(digitalsj,digitalsj+1); } } if(flag){ break; } }

Давайте посмотрим, что мы сделали для ее оптимизации:

1. В строке 17: изменили условие внутреннего цикла на .Поэтому чтобы лишний раз не сравнивать элементы массива тратя на это время, мы решили уменьшать отрезок внутреннего цикла на 1, после каждого полного прохода внешнего цикла.
2. Вы могли заметить, что если даже массив стал отсортирован (или сразу был отсортирован) алгоритм все равно продолжает сравнивать элементы.

Для этого в строке 5: чтобы пузырьковая сортировка останавливалась (когда массив уже стал отсортирован), мы объявили булеву переменную (ее обычно называют флаг или флажок). Еще при ее инициализации мы поместили значение , но она меняется на:

false, если результат условия в строке 4: положительный.

А в строке 9: чтобы мы могли выйти из алгоритма мы проверяем:

• Если булева переменная равна , значит массив уже полностью отсортирован и можно выйти. Для этого используем оператор .
• Если же значение равно , то продолжаем сортировать массив.

В строке 6: вы (возможно) увидели незнакомую функцию . Если коротко описать что она делает, то она принимает два аргумента (через запятую) и меняет их значения местами. В нашем случаи она принимает ячейки и . Мы использовали эту функцию чтобы не писать вот эти 3 строчки:

int b = digitals;
digitals = digitals;
digitals = b;

1 2 3

intb=digitalsj; digitalsj=digitalsj+1; digitalsj+1=b;

Использовать ее необязательно, потому что она не сделает код быстрее. Но как мы сказали выше, кода станет меньше.

2.8 Теоретическое сравнение сортировок методом простых вставок и методом пузырька

Выполним по рекомендованной литературе теоретическое сравнение алгоритмов сортировок, рассматриваемых в данном курсовом проекте. Основным критерием сравнения сортировок является их эффективность, то есть число сравнений и число пересылок. Данные показатели также влияют на время сортировки. Укажем основные формулы, использующиеся для вычисления эффективности данных сортировок:

− число сравнений ключей элементов при i-ом просеивании;

−минимальное число сравнений ключей;

− максимальное число сравнений ключей;

− среднее число сравнений ключей;

− число пересылок (присваиваний) элементов при i-ом просеивании;

− минимальное число пересылок

− максимальное число пересылок

− среднее число пересылок

− размер массива;

Рассмотрим сортировку методом простых вставок

Рассмотрим сортировку методом пузырька

На основе данных методических формул составим сравнительную таблицу для сортировок методом простых вставок и методом пузырька:

Таблица 2. Сравнительный анализ сортировок методом простых вставок и методом пузырька

Размер массива	Метод простых вставок	Метод пузырька
Число сравнений ключей (среднее значение)	Число пересылок (среднее значение)	Число сравнений ключей (среднее значение)	Число пересылок (среднее значение)
32	263	329	256	384
64	1039	1163	1024	1536
128	4127	4379	4096	6144
256	16447	16953	16384	24576
512	65663	131835	65536	98304
1024	262399	264443	262144	393216

На основе полученных в таблице 2 значений составим сравнительные графики, для числа сравнений ключей и для числа пересылок по обоим методам сортировки:

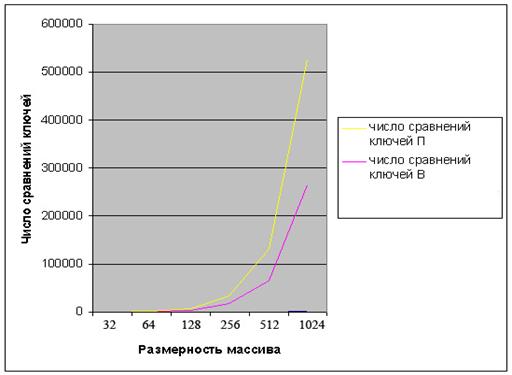
Рисунок 10. Графики числа сравнений ключей: число сравнений ключей П — для метода пузырька, число сравнений ключей В — для метода простых вставок.

На основе полученных графиков можно сказать, что число сравнений ключей в сортировке методом пузырька число сравнений больше, чем в сортировке методом вставок. Следовательно по данному критерию эффективность сортировки методом простых вставок выше, чем методом пузырька.

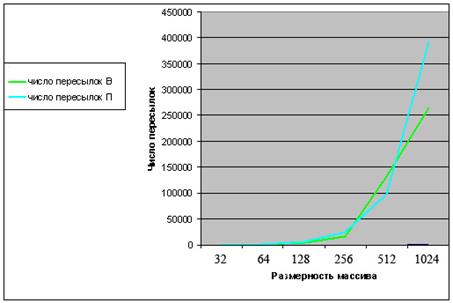
Рисунок 11. Графики числа пересылок в сортировках: число пересылок П — для метода пузырька, число пересылок В — для метода простых вставок.

Основываясь на полученных графиках можно сказать, что при малых значениях размерности массива число пересылок для обоих методов примерно одинаково. При относительно больших размерах массива (от 512 и более) число пересылок в методе

пузырька возрастает быстрее, чем в методе простых вставок. Следовательно, эффективность метода вставок выше по данной характеристике.

Ссылаясь на таблицу 1 можно также отметить, что сортировка методом пузырька требует больше времени, чем сортировка методом вставок.

Из чего следует, что в целом сортировка методом простых вставок эффективнее сортировки методом пузырька.

Тестирование разработанных функций сортировки методом простых вставок и методом пузырька

В ходе работы над курсовым проектом было разработано 2 функции: функция сортировки массива методом простых вставок, и функция сортировки массива методом пузырька. Так же в разработанной программе использована функция подсчета времени работы программы clock (), содержащаяся в библиотеке time. h. Массив формируется автоматически с помощью встроенной функции randomize (), пользователю нужно лишь задать число элементов в массиве и выбрать метод сортировки. После чего будет выполнена сортировка выбранным методом, выведен на экран упорядоченный массив и время сортировки в миллисекундах.

Для тестирования работы программы совершим несколько прогонов с разными значениями. В качестве отчета о работе программы приведены скриншоты:

Рисунок 12. Скриншот работающей программы, сортировка методом простых вставок

Рисунок 13. Скриншот работающей программы, сортировка методом пузырька

Как видно на скриншотах программа успешно выполняет сортировку методом простых вставок и методом пузырька и выводит время сортировки.

Заключение

Метод пузырька гораздо менее эффективен других алгоритмов, однако он имеет простую и понятную реализацию, поэтому часто используется в учебных целях. Кроме того, пузырьковая сортировка может использоваться для работы с небольшими массивами данных.

На самом деле, вместо самостоятельного написания алгоритмов сортировки программисты на Python используют стандартные функции и методы языка, такие как и . Эти функции отлажены и работают быстро и эффективно.

Знания особенностей алгоритмов сортировки, их сложности и принципов реализации в общем виде пригодятся каждому программисту, желающему пройти собеседование и стать Python-разработчиком.